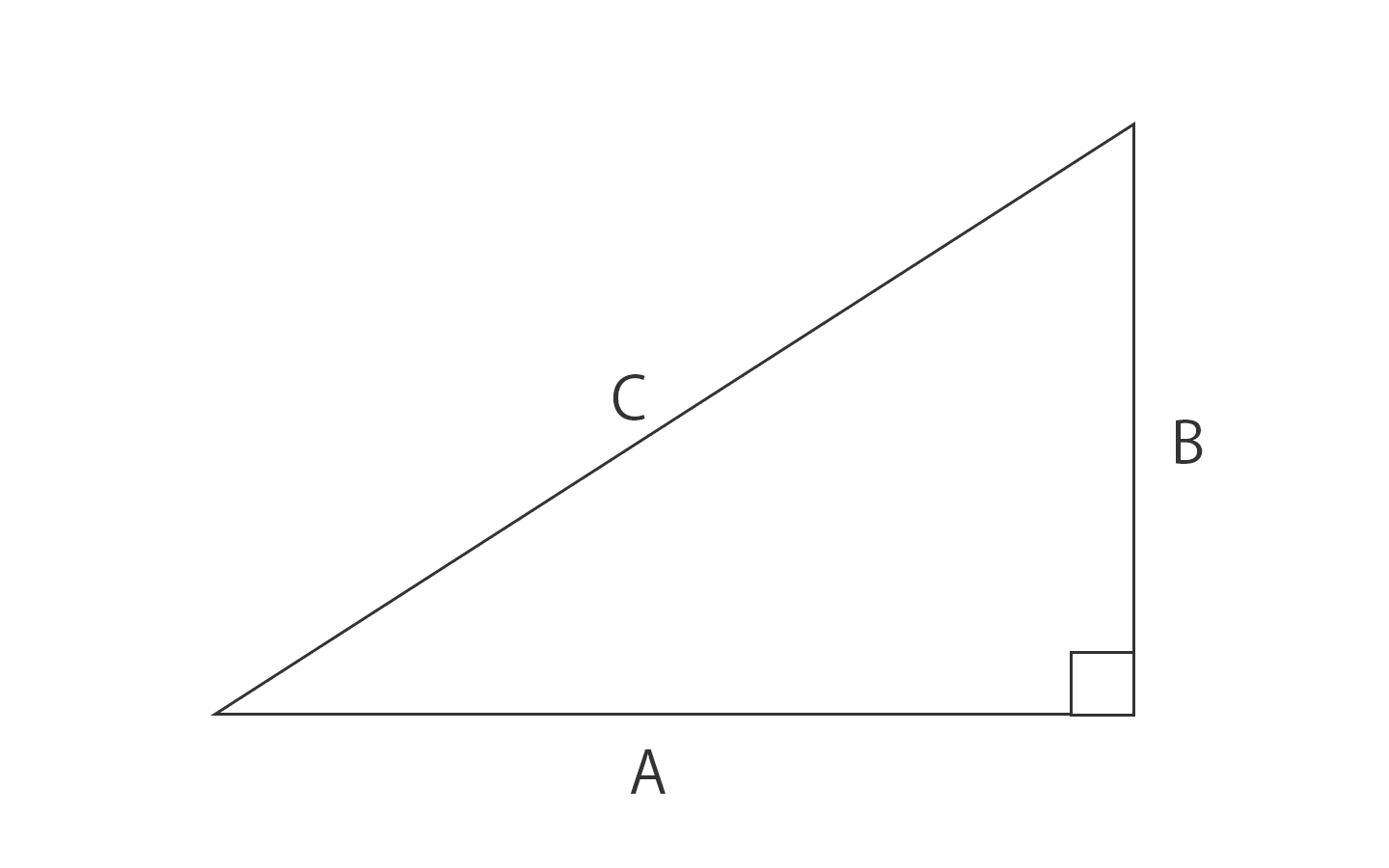
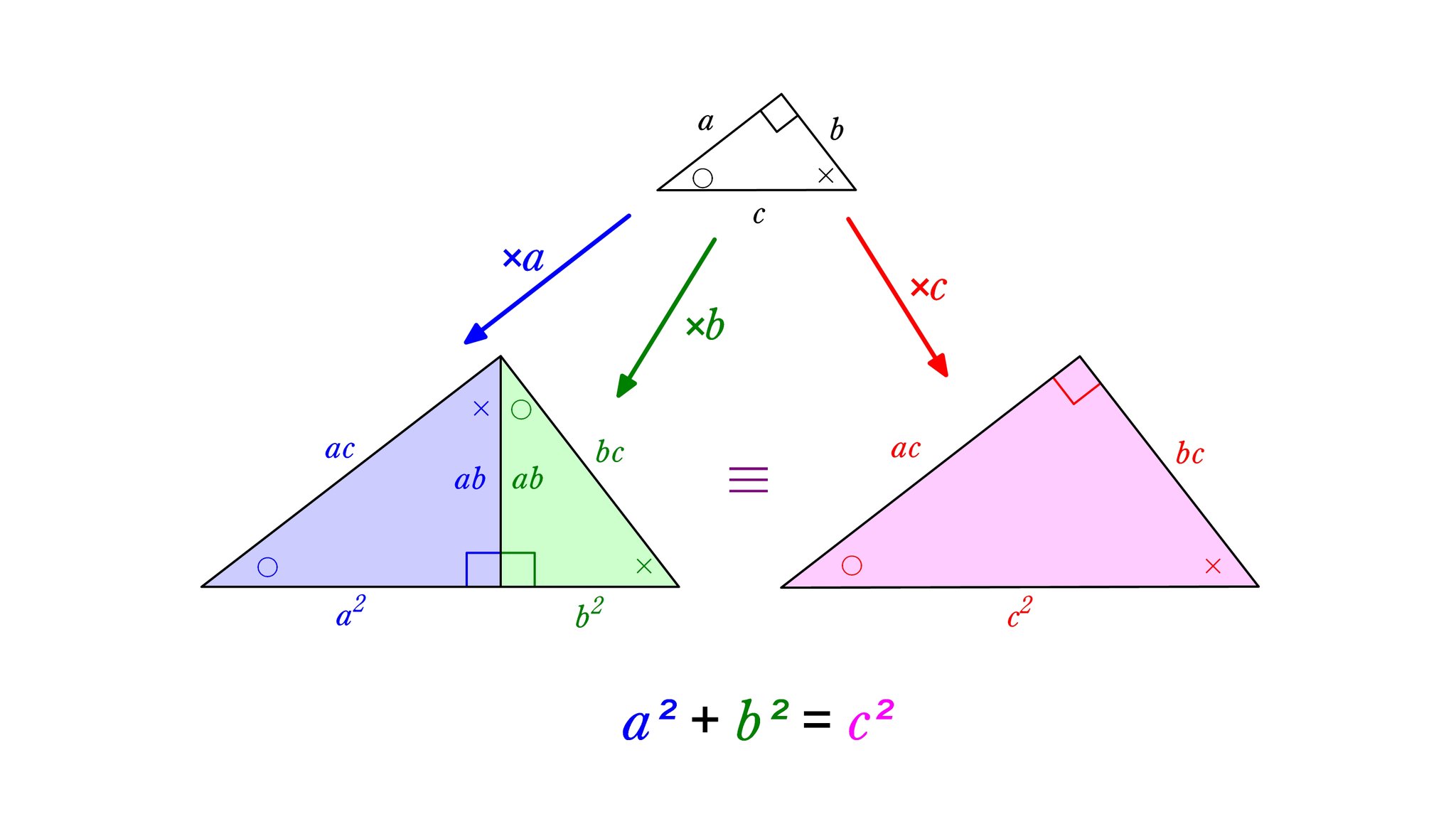
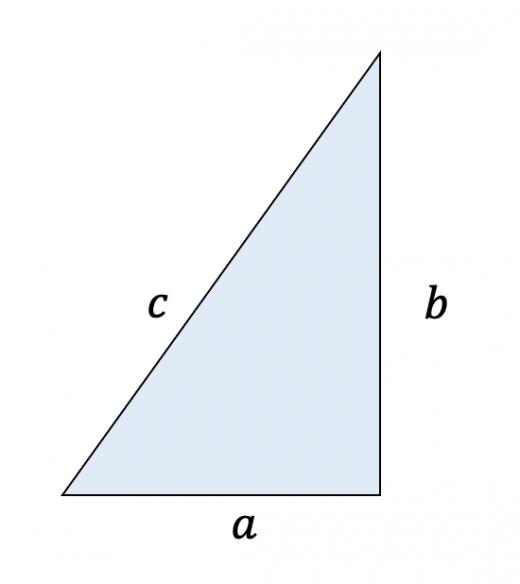
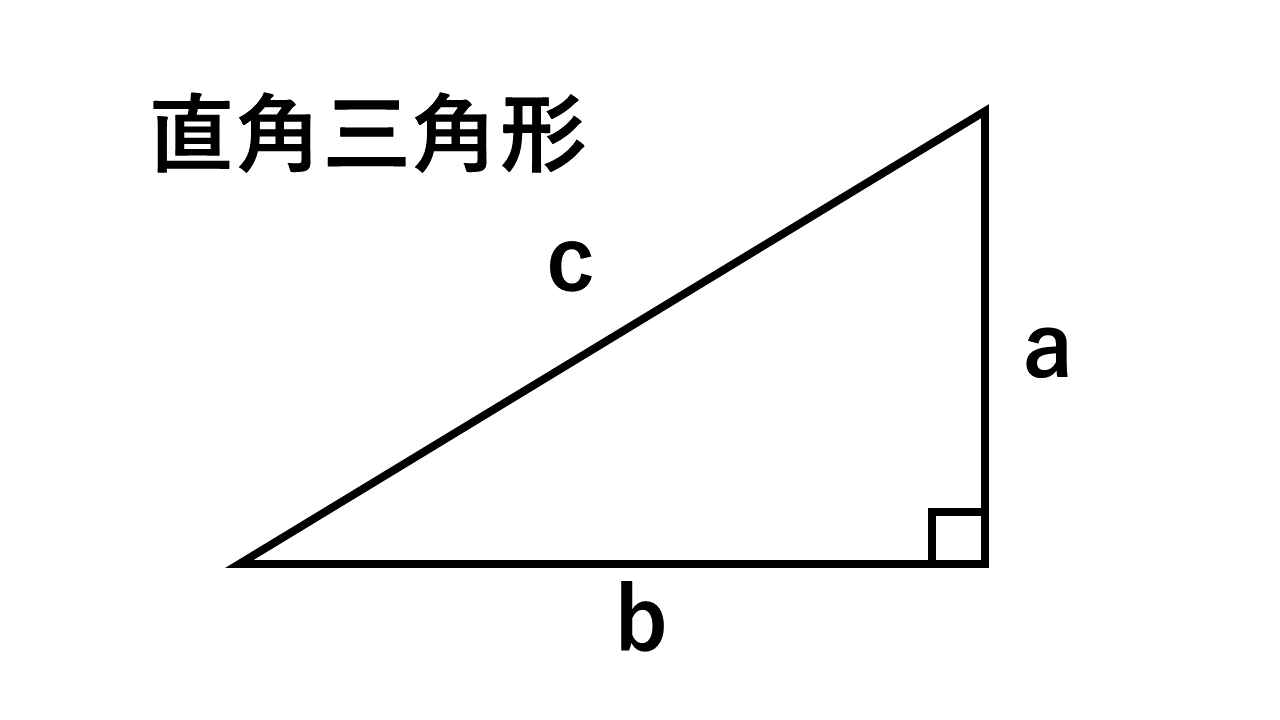
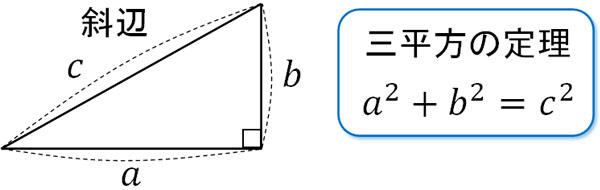
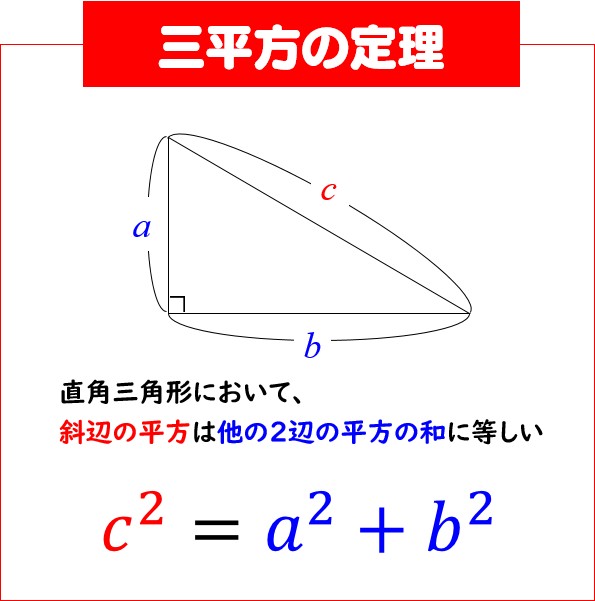
三平方の定理は、直角三角形の3つの辺の長さの関係を表わした定理で、直角三角形の直角を挟む2つの辺の長さをそれぞれ a a 、 b b とし、斜辺の長さを c c とすると、 a2 b2 = c2 a 2 b 2 = c 2 の関係が成り立つ、という定理です。 つまり、三平方の定理は、 直角三角形の直角を挟む2つの辺の長さをそれぞれ2乗して足すと、その値は斜辺の長さを2乗したものと等しくなるよ! みたいな定理
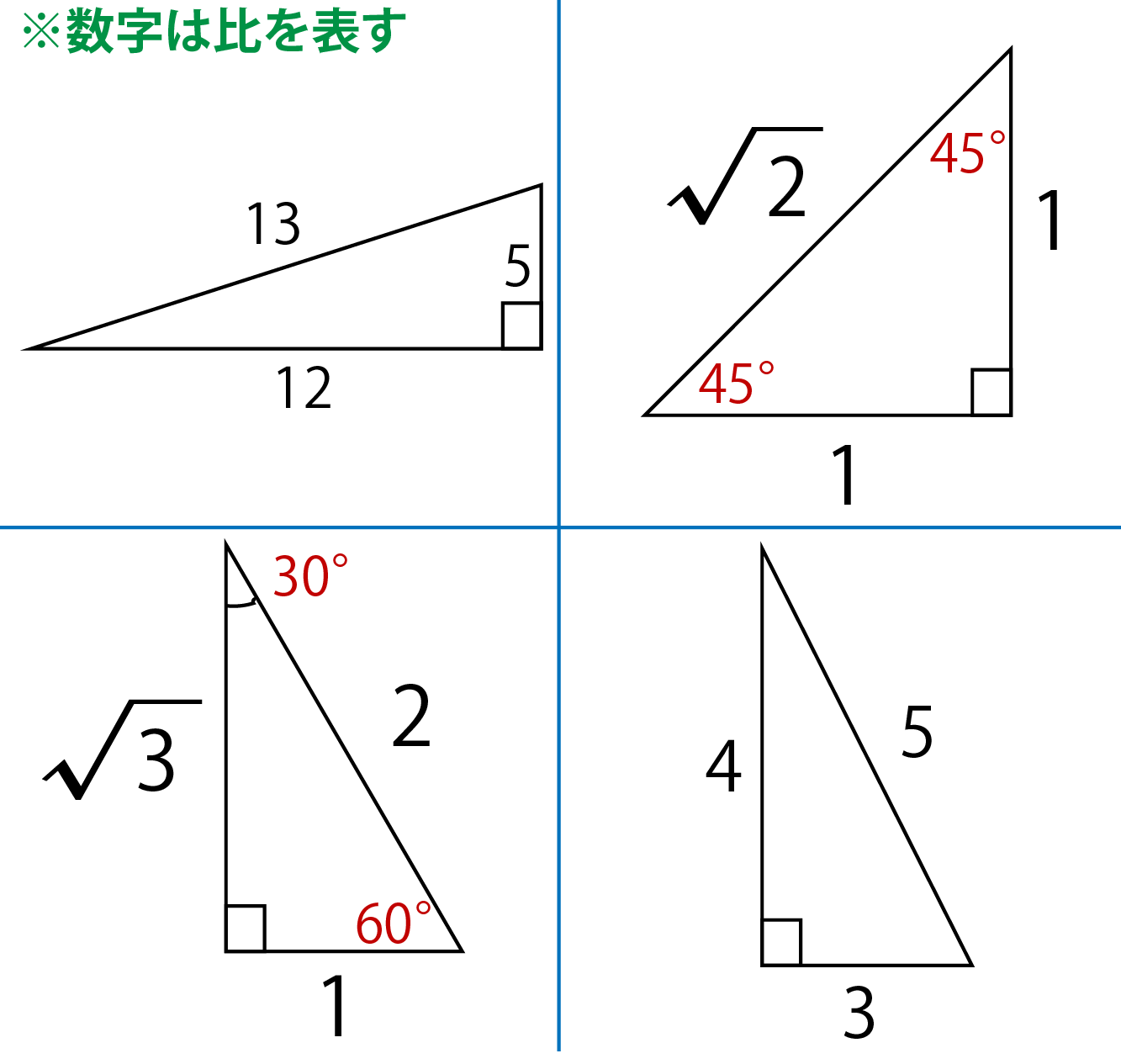
直角 三角形 三 平方 の 定理- が成り立つという有名な定理です ここでは, 三平方の定理 (平面上の定理)を3次元に拡張した, 四平方の定理を紹介します 定理 3つの面が直角三角形で, 1つの頂点に直角が集まっている 三角錐 を考えるとき, 直角三角形の面の面積を S1,S2,S3 S 1, S 2, S 3, 残り三角定規型暗記しておくべき直角三角形があります。それは三角定規の形です。三角定規は \(2\) 種類あります。その \(2\) 種類は必ず暗記すべき特別な直角三角形です。45° 45° 90°まずはじめに直角二等辺三角形タイプです。
直角 三角形 三 平方 の 定理のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  | |
 |  | |
 |  | |
「直角 三角形 三 平方 の 定理」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「直角 三角形 三 平方 の 定理」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
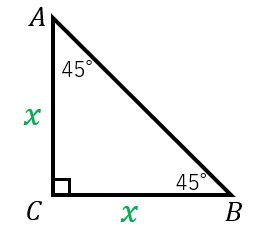 |  |  |
 |  | |
 |  | |
「直角 三角形 三 平方 の 定理」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 | ||
 |  |  |
「直角 三角形 三 平方 の 定理」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  |  |
「直角 三角形 三 平方 の 定理」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 | ||
「直角 三角形 三 平方 の 定理」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  | |
「直角 三角形 三 平方 の 定理」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  |  |
「直角 三角形 三 平方 の 定理」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |
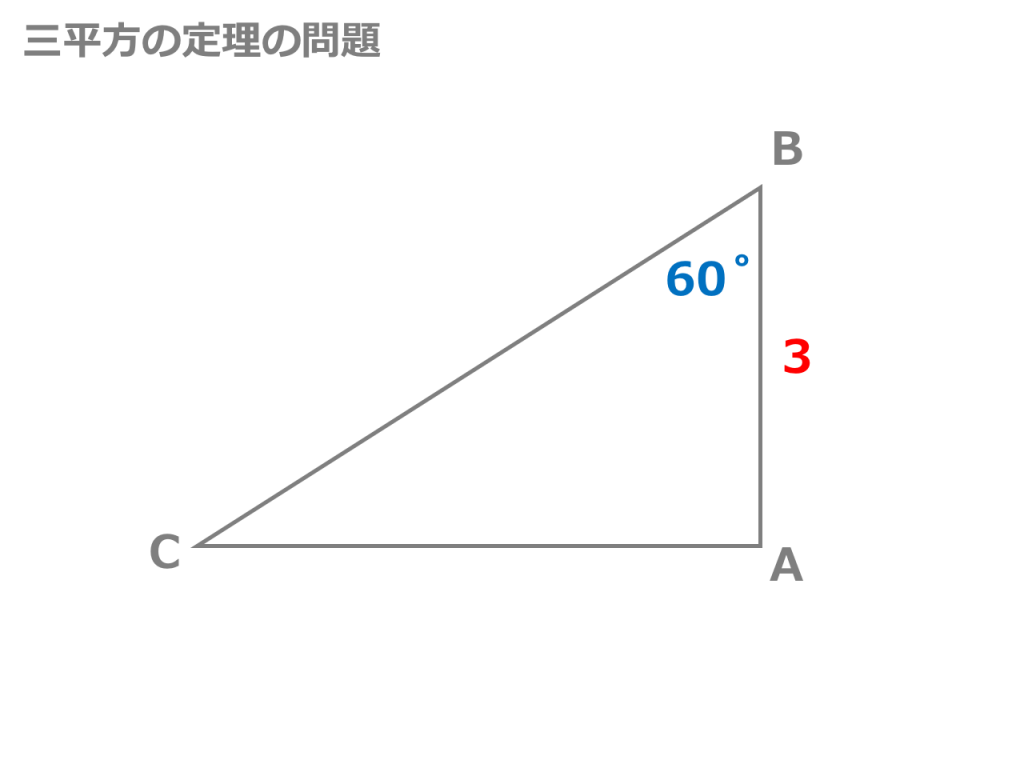
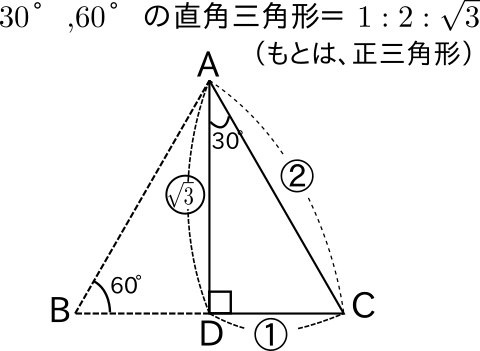
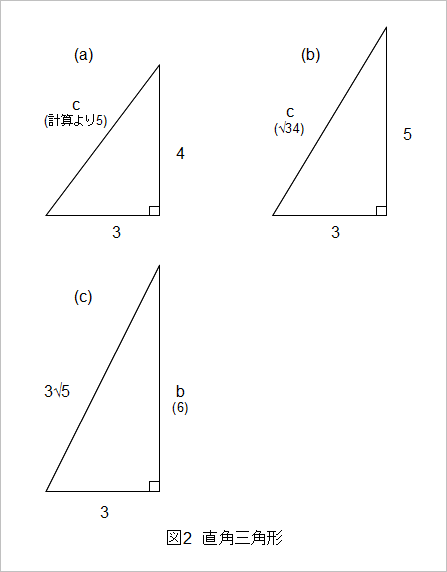
(4)如果两个实数相等,那么它们的平方相等;解:逆命题是: ;它是 命题。二、自主学习1、勾股定理是直角三角形的 定理;它的逆定理是直角三角形的 定理2、请写出三组不同的勾股数: 、 、 3、借助三角板画出如下方位角所确定的射线1辺3㎝の正四面体の体積と表面積を求めよ。 表面積 1辺3cmの正三角形の面積を出す。 頂点aから辺bcに垂線amを引くと abmは30°、60°、90°の直角三角形となる。 ab=3なのでabam=2 3 より am = 3 3 2 これが abcの高さなので 面積 abc = 3× 3 3 2 ÷2= 9 3 4 正四面体は各面が





0 件のコメント:
コメントを投稿