データの分析無理数の近似値の求め方 標準偏差を求める問題の解答の最後に, √4=142 とあるのですが,なぜそのようになるのかわかりません。 進研ゼミからの回答 こんにちは。 いただいた質問について,さっそく回答させていただきます。 質問の確認 標準偏差を求める あなたがもしものさしを持っているならば、 長さを図る だけで √2 を求められます。 ものさしの精度は高いほど、良い近似値が得られるので、なるべく精巧なものさし を用意しましょう! 1 折り紙 最も身近な √2 です! 三平方の定理 を使いましょう本当に $\sqrt{2}$ の値を深く求めたいのであれば,やり方を変えた方がよさそうです。 図形から求める (中3) 直角をはさむ辺の長さが1の直角二等辺三角形を考えます。そうすると斜辺の長さが $\sqrt{2}$ ですから,それを精密に求めようとすれば $1414\cdots$ が得られるはずです。 右の図の
数学切り抜き帳
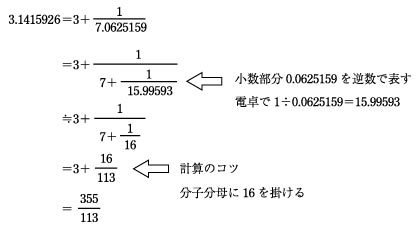
近似値 求め方 テイラー展開
近似値 求め方 テイラー展開-動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru関数の近似とTaylor 展開 係数の求め方 f(x) がn−1 次多項式の場合は(x−x0) で括 ることによって f(x) = a0 a1(x−x0)a2(x−x0)2 ··an−1(x−x0)n−1 と書ける。 このとき を最も良く近似している 次多項式は当 然 そのものである。従って を上のように書いたと




Studydoctor近似値と誤差とは 中学1年数学 Studydoctor
こういう時は、小数点第 1 1 位で四捨五入した値、つまり「 近似値 」を考えます。 体重 585 ( k g) 585 ( k g) → 約 59 ( k g) 59 ( k g) 身長 1721 ( c m) 1721 ( c m) → 約 172 ( c m) 172 ( c m) また、日によって体重や身長はわずかながら変化します。 でも、体重であれば 58 58 の部分、身長であれば 172 172 の部分は変わらない、と言える時があると思います。 こういうとき 平方根の近似値の求め方って? 平方根の近似値を求めるには、どうすればいいのでしょうか。 \(\sqrt{2}\)の近似値を求めてみましょう。 まずは\(\sqrt{2}\)の整数部分 1 整数の部分のことです。例えばという数があったとすると、この整数部分は13、小数少し話がそれてしまったが, 要するに, 身も蓋もない言い方をしてしまえば, どこまでも正確に述べる ことが必ずしもありがたいことではなく, 適度に近しい値を知ることができれば十分であり, その手法が近似と呼ばれているのである 「近似とは何か?
Log102の求め方 – 対数表によると、log102は約0301だというこ – Yahoo!知恵袋次の近似値を求めなさい。√2 や √ の近似値が書いてあるのは、 ★ どちらかを使いなさい という意味ですね。 たとえば、 √0 を、√2 か、√ で表せないか? ( √2× 、√× の形にできないか?) と考えるのがポイントです。最近の投稿 超実数のイメージがわくように説明するよ 数列の「自明な収束」と「自明でない収束」 数学のお兄さんで知られている横山さんが作ったクイズ本の効果 集合の集合
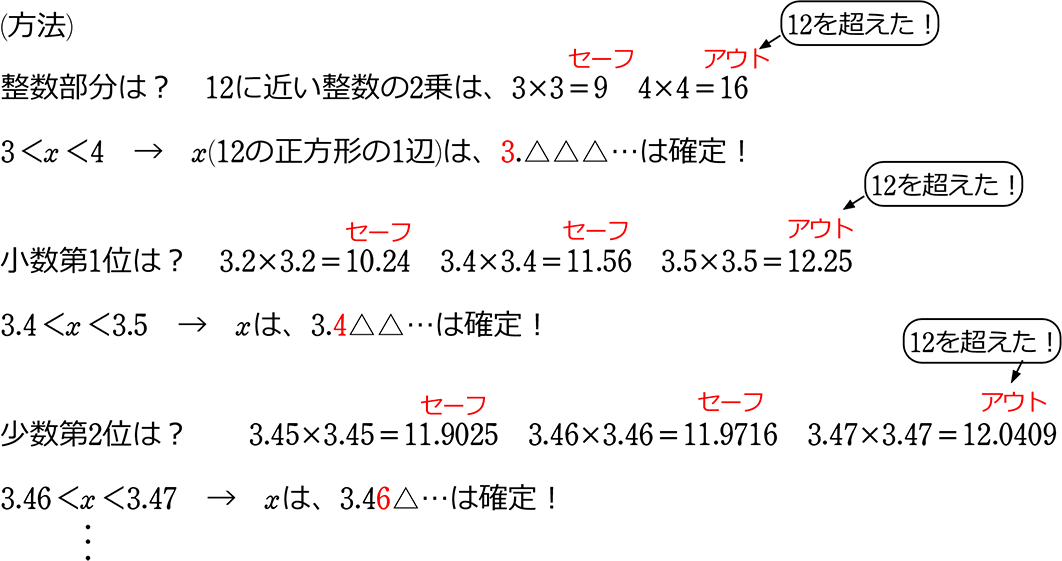
平方根の値を求める方法は,中学校数学では素因 数分解して求める方法と近似値法が一般的である。 しかし,素因数分解が困難(=値の大きい素数の平 方)な場合は,近似値法を使わざるを得なくなる。 近似値法はおおよその値を予想して,何回も平方を散布図のマーカー(右図では青の点)の1つを右クリックし,「近似曲線の追加」→「線形近似」 (3) 図1の (3) (4) 回帰直線,相関係数Rの2乗 を表示するには: 1 グラフ中の「近似直線」を右クリック→「グラフに数式を表示する」「グラフにRー2乗値を表示する」をチェック→OK (これらの式はテキストボックスなので,適当な場所に移動して見やすくすることが7回程度の分数計算で無理数の近似値が求まるが、これが「速いか遅いか」は判断の分 かれるところである。 してみた。(但し、初期値として、X=1 と設定) 実行結果 表計算ソフト Excel のVBAスクリプト Sub 平方根3の近似() Dim N, X As Variant N = 1 X = 1 Range("A1")Select Do Until Abs(X ) < 1E14




中学1年生 数学 資料の活用 近似値と有効数字 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




高校数学 対数log Abの近似値求め方 評価の方法 受験の月
近似値の求め方が分かりません」 平方根の「近似値」の問題ですね。 大丈夫、コツがあるんですよ。 √の中が小数の時は、 小数を分数になおすと、 近似値を求められるんです。 以下で解説していきますね。 まずは準備体操を!近似値きんじち 真 の 値 に 近 い値をいい、測定や近似計算によって得られる。 たとえば15℃の空気中の音の速さの近似値は毎秒340メートル、分数1/3の近似値は033、 円周率 の近似値は314などである。 近似値と真の値の 差 (近似値)-(真の値) を誤差という。 近似値が真の値より大きいときは、誤差は正の数となり、近似値が真の値より小さいときは、誤差データの最終のX値は25なので、30か月後は(3025=5)区間先になります。 近似曲線が30まで伸ばされました。 計算値を求めてグラフに追加してみます。 数式はy=x^ となっていますので、30か月後を予測するためxに30を入れて計算してみます。



関数電卓なしで Ln9の近似値を計算する方法を教えてください L Yahoo 知恵袋




2の近似値の求め方の説明の意味が分かりません Clear
測定値や四捨五入して得られた数字は近似値である。 誤差 近似値と真の値の差を誤差という。 誤差=近似値ー真の値 四捨五入 1245を小数第1位で四捨五入すると12,小数第2位で四捨五入すると125である。 どのけたを四捨五入するかによって誤差や真の値 ルートの近似値の求め方 a \sqrt{a} a の近似値の求め方の概要: x 2 ≒ a x^2≒a x 2 ≒ a となりそうな簡単な x x x を探す。 常用対数log_10 7 の近似値に関する一考察(結川@豊岡高) 数研出版;




中1 数学 中1 近似値 Youtube




中3数学 平方根の近似値 Youtube
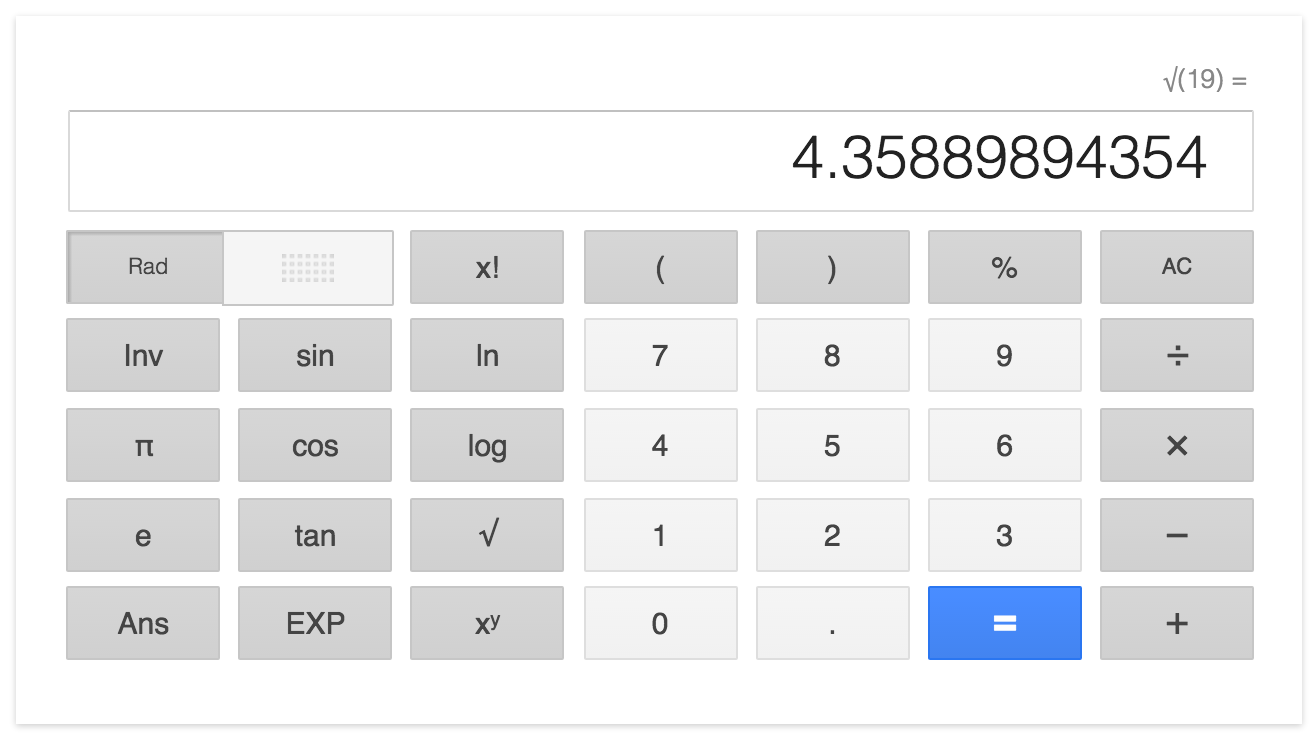
データの分析無理数の近似値の求め方 無理数の近似値の求め方 標準偏差を求める問題の解答の最後に, √4=142 原始的な方法ですが,円は正多角形の極限なので,正多角形の周の長さや面積を用いて円周率の近似値を計算することもできます。 例えば,正 2 n 2^n 2n 角形の周の長さを考えることで, π ≒ 1 2 ⋅ 2 n 1 sin 2 π 2 n 1 = 2 n sin π 2 n \pi\fallingdotseq \dfrac {1} {2}\cdot 2^ {n1}\sin\dfrac {2\pi} {2^ {n1}}\\ =2^n\sin\dfrac {\pi} {2^n} π ≒ 21 平方根(ルート)の近似値の求め方 √2≒141 というのは聞いたことがありますか? 平方根を、近い大きさの数である「近似値」で表せ、という問題はよく出題されます。ここではこの、「平方根の近似値」について説明します。 覚えるべき近似値




中学数学 3分でわかる 平方根の近似値の求め方 Qikeru 学びを楽しくわかりやすく




Pの近似値について 身勝手な主張
図1-2 近似直線の求め方 さて、求まった値が正しいことを確認するには、処理データの散布図を作成し、近似直線を求め、その式の係数とaを、定数とbを見比べます。 図1-3 グラフから求める近似直線 02 ルートの近似値 続いて次の値の近似値を求めてみましょう! まず次のように変形します: すると x = 7/121 = を微小量 x とみなして、先ほど求めた近似式を用いることができます: 右辺を計算することで √128 の近似値が求まりました!近似値を求める問題の解き方 近似値を求め方のやり方が教科書に書いてなかったので質問させてください。 √2=1414 √3=1732とするとき、近似値を求めなさい 例えば√0の場合はどのようにして近似値を求めるのでしょうか?




平方根 式の値 求め方はどうやる 問題を使って徹底解説 数スタ



近似値の問題 苦手な数学を簡単に
平均値の求め方・近似値・真の値・誤差の求め方中学1年数学:資料の分析と活用 ルート3の近似値の求め方4パターン EXCELの作業で悩み・お困りごとはありませんか? 集計に時間がかかり過ぎ。 21 1 N1000 Value3 さらに、1 Excel07、10ではVBAを使う必要がありました。 「グラ 開平法 (ルートの近似値の求め方) /2/5 1800 古式ゆかしい珠算 (そろばん)の手法で、ルートの近似値を求める開平法という方法があります。 ちなみに、かなり難しいです。 珠算で言うと段位の取得の際に習うのかな、ちなみに私は1級。 ならったけどただ、近似曲線を表示したものの式が出ていないことがあります。 ここでは、近似曲線の計算式を表示させたり、近似曲線から値を求める方法について解説していきます。 ・近似曲線を表示させる方法の式を出す方法 ・近似曲線の数式から値を求める方法




中学数学 近似値 有効数字 から誤差を求める1つの方法 Qikeru 学びを楽しくわかりやすく



平方根 ルート の計算や問題の解き方を完璧に理解しよう Studyplus スタディプラス
π の近似値 このページでは過去発表された円周率の近似値を表す数式を紹介する。 元の表記方法(の日本語訳)をそのままを使うと(特に古い文献で) 円周率を求めた記述ではないというような解釈ができるが ここでは π = π = の形に解釈したものを表記する。 例えば「円の直径が 1 のとき、その円の円周は 3 である」 という様な記載がなされていれば π = 3 π常用対数について – 常用対数を関数電卓を使わずに正確に計算する方法 – Yahoo!知恵袋; 近似値の求め方がわかりません 解説よろしくお願いします Clear 開平法のやり方と原理 高校数学の美しい物語 中学1年生 数学 資料の活用 近似値と有効数字 練習問題プリント 中学数学 近似値 有効数字 から誤差を求める1つの方法 Qikeru 近似値から真の値の範囲を求める 数学解説ブログ




中学1年生 数学 資料の活用 近似値と有効数字 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




Studydoctor近似値と誤差とは 中学1年数学 Studydoctor
Eの近似値を求める(紹介) レポート 29 年11 月25 日(土) アスティ45 ビル 千歳科学技術大学 安田富久一 本研究会第102 回でe の値を求めるレポートを発表した。その後、『高校数学と大学数学の接点』 佐久間一浩(著)・日本評論社、に前回紹介したものより簡単で、しかもよりよい評価が得 指数近似は、後から出てくる累乗近似と似ています。 これは、縦軸に対数をとる片対数グラフで活躍します。 線形近似 これは、最も一般的に使われる近似なのではないでしょうか。 小学校か中学校で習う「y=axb」という式の直線が引けます。 値が、一定のペースで増加または減少する場合に使います。 対数近似




近似 値 求め 方 近似値 Documents Openideo Com




高校数学 近似値 平方根 円周率 常用対数 自然対数の底 のゴロ合わせ 受験の月




50 近似 値 求め 方 ニーアオートマタ 壁紙
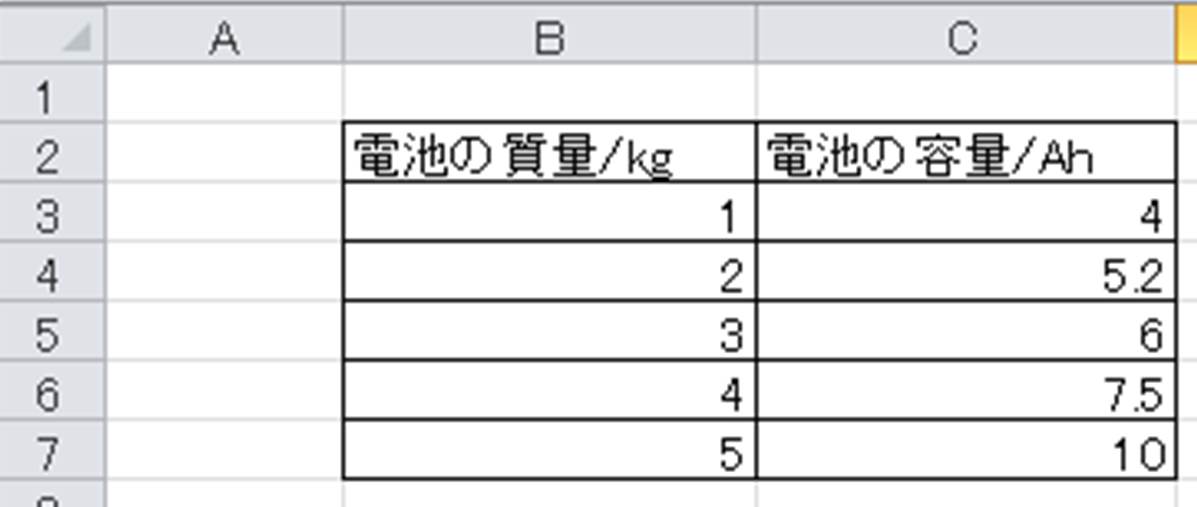



Excel エクセルで表示した近似曲線の式を出し 数式から値を求める方法




中学数学 近似値 有効数字 から誤差を求める1つの方法 Qikeru 学びを楽しくわかりやすく




中学数学 3分でわかる 平方根の近似値の求め方 Qikeru 学びを楽しくわかりやすく




数学切り抜き帳




近似値と有効数字の求め方とは どちらも情報の 度が大事 遊ぶ数学
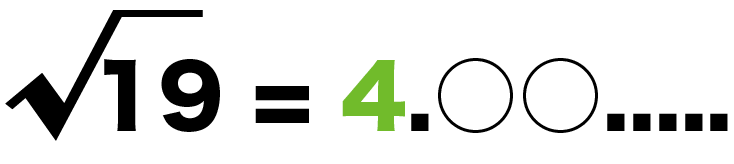



中学数学 3分でわかる 平方根の近似値の求め方 Qikeru 学びを楽しくわかりやすく




近似値の求め方がわかりません 解説よろしくお願いします Clear




円周率を紙とペンで計算する 柞刈湯葉 Yuba Isukari Note




中3数学 平方根の近似値 映像授業のtry It トライイット
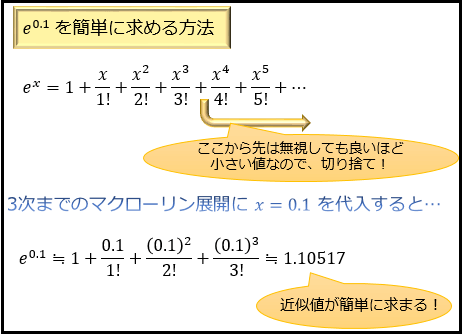



テイラー展開 マクローリン展開はどう使うのか 関数をシンプルに考える近似のテクニック アタリマエ




ルートの近似値の求め方 中3数学 Youtube
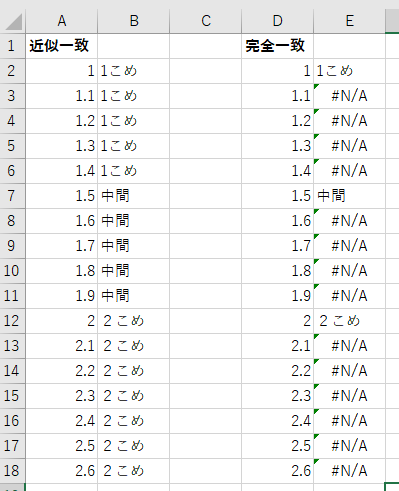



Vlookup関数の 近似値 条件true の実際の動作を 徹底検証する 志木駅前のパソコン教室 キュリオステーション志木店のブログ



1



1




わかる授業動画 中学3年数学 平方根 第30回 の近似値の求め方 000 00 0 02 0 2 32の近似値は Youtube



ルートを開こう




ニュートン法の例題 ルート3の近似値を与える方法 理数アラカルト




平方 数 語呂合わせ 100までの 平方数 一覧表と性質や特徴 小学生 中学受験の算数 Amp Petmd Com




中1数学 近似値 練習編 映像授業のtry It トライイット



近似値 近似式とは 公式や求め方 テイラー展開 マクローリン展開も 受験辞典




平方根とは 東大生が平方根の計算方法や覚え方を伝授 高校生向け受験応援メディア 受験のミカタ
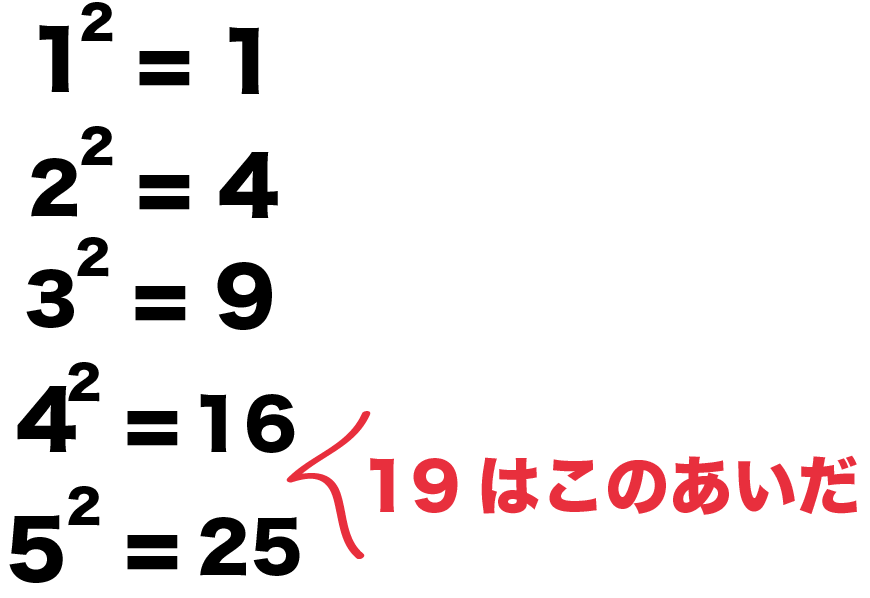



中学数学 3分でわかる 平方根の近似値の求め方 Qikeru 学びを楽しくわかりやすく




中1 数学 近似値の考え方や求め方 中学生 数学のノート Clear




6 の正しい近似値を教えてください 左がネット 右が教科書 です Clear




データの分析 無理数の近似値の求め方 数学 定期テスト対策サイト




ルート2 ルート3 ルート5の覚え方など 高校数学の美しい物語




円周率の 一風変わった 近似式 Tsujimotterのノートブック




数学 近似式まとめ 各種公式 求め方 理系ラボ




中学数学 近似値 有効数字 から誤差を求める1つの方法 Qikeru 学びを楽しくわかりやすく
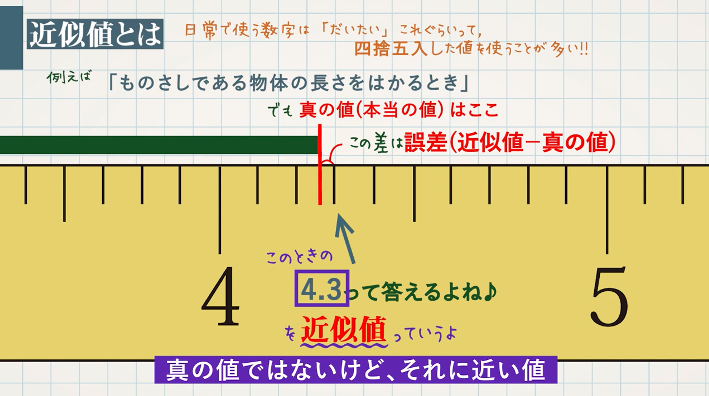



近似値と有効数字 教遊者



平均値の求め方 近似値 真の値 誤差の求め方 中学1年数学 資料の分析と活用




もう円周率で悩まない Pの求め方10選 プロクラシスト




平方根のおよその値の求め方とその利用 わかるようになる高校数学



数 近似値 近似式 数学のコツ




中学数学 3分でわかる 平方根の近似値の求め方 Qikeru 学びを楽しくわかりやすく
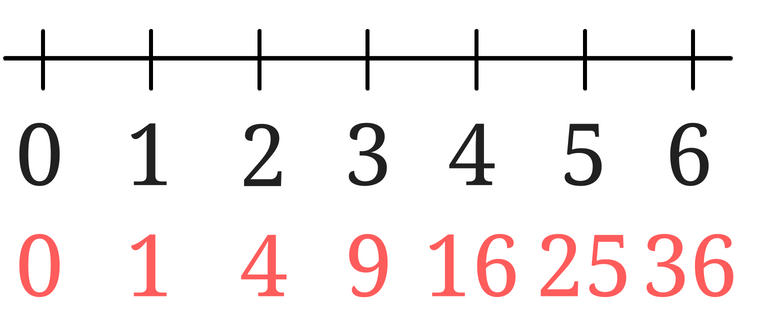



平方根の近似値を求めるにはどんな考え方をするの 語呂合わせを使った覚え方は さびねこ中学校




ニュートン法の例題 ルート3の近似値を与える方法 理数アラカルト



Studydoctor ルートの近似値の求め方 中3数学 Studydoctor




数学 近似式まとめ 各種公式 求め方 理系ラボ




近似値から真の値の範囲を求める 数学解説ブログ つくば市の 数学 算数 物理に強い プロ家庭教師 長通幸大 発信



近似値ってどうやって求めるんでしたっけ そもそも近似値と Yahoo 知恵袋
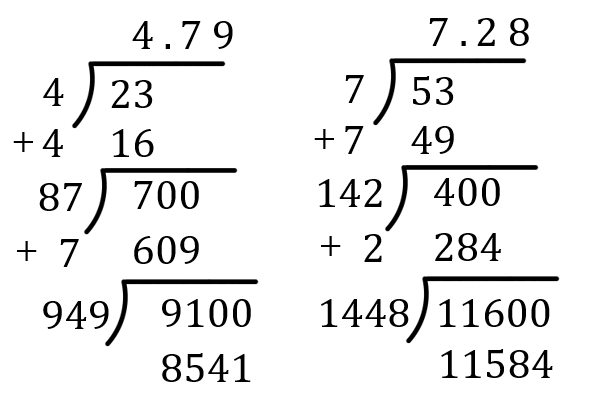



ルート2ルート3ルート5ルート7のゴロ合わせ 素数の平方根の筆算の仕方 アタリマエ




数学切り抜き帳




高校数学 関数f X の1次近似式 映像授業のtry It トライイット




微分法とその応用 の記事一覧 受験辞典




中学数学 3分でわかる 平方根の近似値の求め方 Qikeru 学びを楽しくわかりやすく




ルートの近似値を計算する素朴な方法とコツ 高校数学の美しい物語




中1数学 近似値 練習編 映像授業のtry It トライイット




ルート3の近似値の求め方4パターン 数学の星




中3 数学 平方根12 近似値を使う計算 4分 Youtube



60の近似値の求め方を教えてください 電卓を使う ではダメでしょうね Yahoo 知恵袋




平方根の活用 式の値と近似値の求め方 教遊者
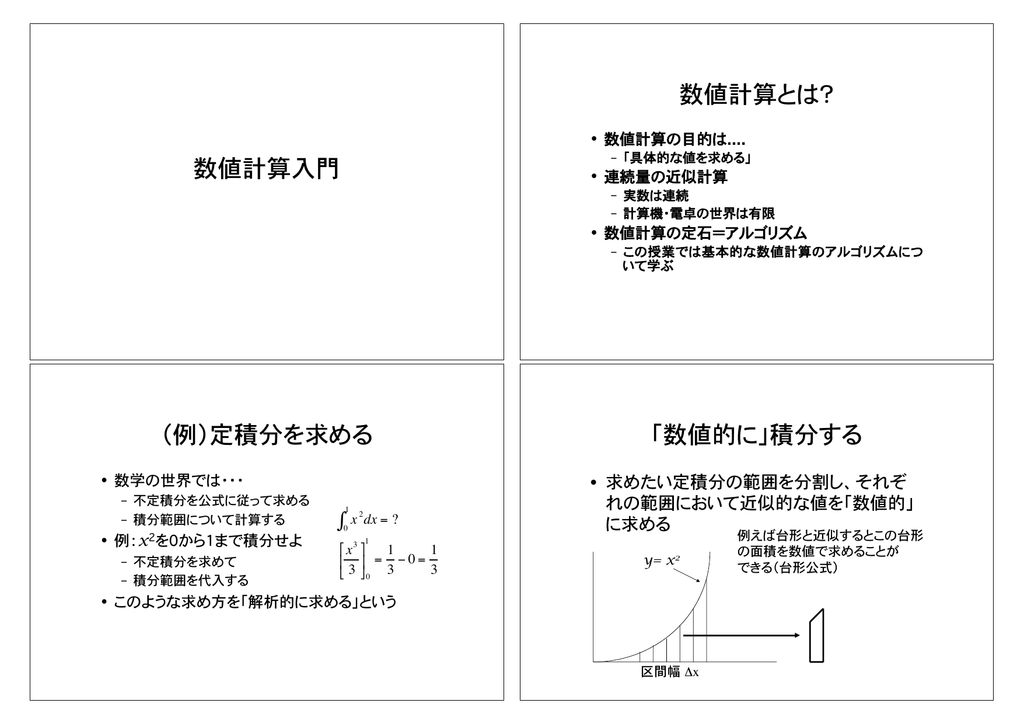



ガイダンス




中1数学 有効数字 近似値と誤差の要点と定期テスト対策問題 Examee




Newton法とは 近似値の求め方 うさぎの日常




1枚目と二枚目の真の値の求め方聞かれてるのは一緒なのに解き方ちがうとおもんですが Clear



平方根とは 計算方法や求め方 近似値の覚え方 利用問題 受験辞典




もう円周率で悩まない Pの求め方10選 プロクラシスト




中1数学 近似値と誤差の求め方の定期テスト予想問題 Pikuu
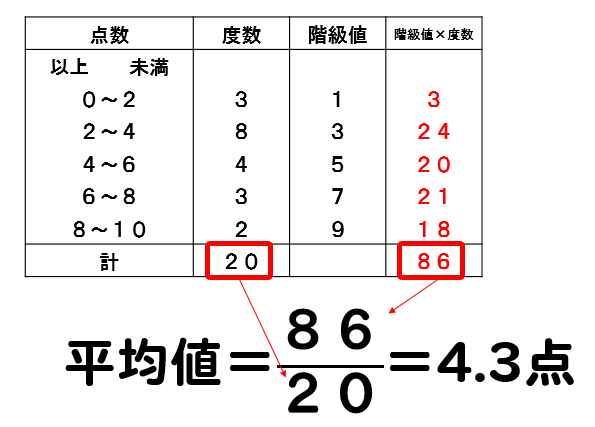



中1数学 資料の活用まとめ 用語の意味と求め方を徹底解説 数スタ




中3数学 近似値を使う計算 映像授業のtry It トライイット




平方 数 語呂合わせ 100までの 平方数 一覧表と性質や特徴 小学生 中学受験の算数 Amp Petmd Com




Log10 2からlog10 5を求める方法は Log10 2 A Log10 3 B とする時のlog10 15の計算方法は Log2 10 の 近似値の覚え方 ウルトラフリーダム




6 の正しい近似値を教えてください 左がネット 右が教科書 です Clear



68 08の小数点以下の近似値の求め方を教えてください Yahoo 知恵袋




中3 ルートの近似値の求め方をイチから解説 Youtube



中学数学 3分でわかる 平方根の近似値の求め方 Qikeru 学びを楽しくわかりやすく



3




中学数学 近似値 有効数字 から誤差を求める1つの方法 Qikeru 学びを楽しくわかりやすく




中学数学 近似値 有効数字 から誤差を求める1つの方法 Qikeru 学びを楽しくわかりやすく




近似式とは 練習問題で微分の応用を理解しよう 高校生向け受験応援メディア 受験のミカタ



Excel10 16 範囲から近似値を求めるには 教えて Helpdesk




近似値と有効値 数学の要点まとめ 練習問題一覧




高校数学 近似値の計算 問題編 映像授業のtry It トライイット



中学数学 平方根



近似式 京極一樹の数学塾




近似値とはどういうことでしょうか どなたか教えてください Clear




ルートの近似値を計算する素朴な方法とコツ 高校数学の美しい物語




近似値計算関数の性能を検証する Oracle Database 18c Qiita



3




平方根 近似値を求める 苦手な数学を簡単に




6 2 449 60 7 746として次の 3 4 の近似値の求め方を教えて Clear




中1数学 近似値 練習編 映像授業のtry It トライイット




高校数学 近似値の計算 問題編 映像授業のtry It トライイット



中学数学 3分でわかる 平方根の近似値の求め方 Qikeru 学びを楽しくわかりやすく



平方根の活用 式の値と近似値の求め方 教遊者



第2章10平方根 平方根の近似値 フロントエンドなブログ



0 件のコメント:
コメントを投稿