You can also solve for x in terms of y but it is simplier to solve y instead 2 Substitute for that variable in the other equation Solve >Match the given equation with its graph 4x^2 y^2/25 z^2 = 1 Choose the correct graph below Get more help from Chegg Get 11 help now from expert Calculus tutors Solve it with our calculus problem solver and calculator1 Choose any of the preset 3D graphs using the drop down box at the top 2 You can enter your own function of x and y using simple math expressions (see below the graph for acceptable syntax) 3 Select Contour mode using the check box In this mode, you are looking at the 3D graph from above and the colored lines represent equal heights (it's just like a contour
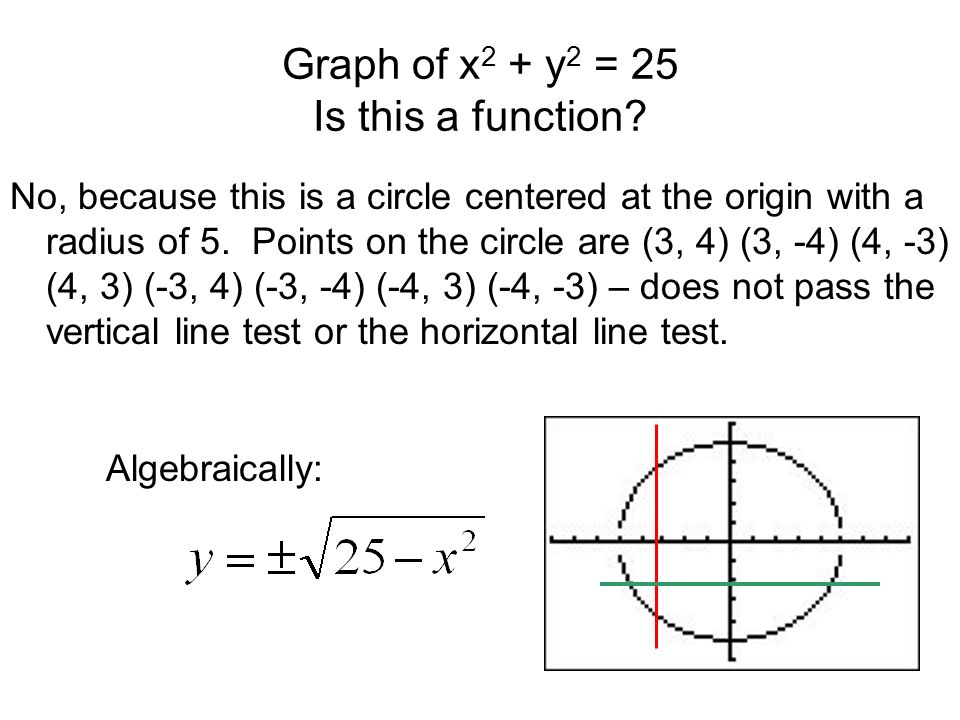
Properties Of Functions Y F X Read Y As A Function Of X X Values Independent Variables Y Valuesdependent Variables Domain Of Fall Possible Inputs X Ppt Download
Graph the circle x^2+y^2-10x-10y+25=0
Graph the circle x^2+y^2-10x-10y+25=0-Click here to see ALL problems on Quadraticrelationsandconicsections Question x^2/25y^2/16=1 How to graph that ellipse?Find the center, transverse axis, vertices, foci, and asymptotes for the hyperbola
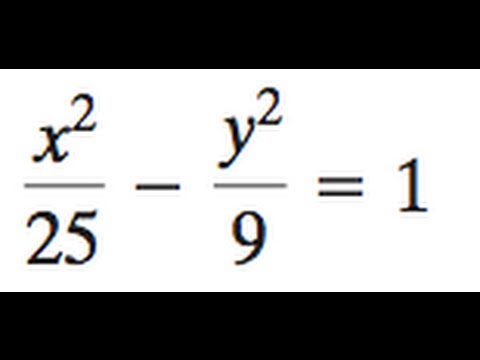



Hyperbola X 2 25 Y 2 9 1 Youtube
Question What Kind Of Graph Is X^2y^2z^2=9 This problem has been solved!Graph a e = {(x, y) 16 x 2 y 2 25} graph b e = {(x, y) 16 x 2 y 2 25} graph c e = {(x, y) 16 x 2 y 2 25} graph d e = {(x, y) 16 x 2 y 2 25} graph e e = {(x, y) 16 x 2 y 2 25} graph f e = {(x, y) 16 x 2 y 2 25} graph g e = {(x, y) 16 x 2 y 2 25} graph hGraph a circle (a conic section) given in standard form and label the intercepts Steps and notes for graphing conic sections playlist https//wwwyoutubec
Which of these graphs shown represents x^2 y^2 = 225 2 See answers adriennedjohnson06 adriennedjohnson06 The answer is C Hope this helped What's part B of the question mehdibenbrahim12 mehdibenbrahim12 Answer C Stepbystep explanation the answer is c New questions in MathematicsHow To Given the standard form of an equation for an ellipse centered at (0,0) ( 0, 0), sketch the graph Use the standard forms of the equations of an ellipse to determine the major axis, vertices, covertices, and foci Solve for c c using the equation c2 = a2 −b2 c 2 = a 2 − b 2Graph x^2y^2=4 x2 − y2 = 4 x 2 y 2 = 4 Find the standard form of the hyperbola Tap for more steps Divide each term by 4 4 to make the right side equal to one x 2 4 − y 2 4 = 4 4 x 2 4 y 2 4 = 4 4 Simplify each term in the equation in order to set the right side equal to 1 1 The standard form of an ellipse or hyperbola requires
Sin (x)cos (y)=05 2x−3y=1 cos (x^2)=y (x−3) (x3)=y^2 y=x^2 If you don't include an equals sign, it will assume you mean =0 It has not been well tested, so have fun with it, but don't trust it If it gives you problems, let me know Note it may take a few seconds to finish, because it has to do lots of calculationsSteps to graph x^2 y^2 = 4Multiply 1 − 1 by 0 0 Add 25 25 and 0 0 Substitute the values of a a, d d, and e e into the vertex form a ( x d) 2 e a ( x d) 2 e Set y y equal to the new right side Use the vertex form, y = a ( x h) 2 k y = a ( x − h) 2 k, to determine the values of a a, h h, and k k




Convert The Rectangular Equation To Polar Form And Select Its Graph X 2 Y 2 25 Study Com



Square Root Hat Ti Exercise
Knowledgebase, relied on by millions of students &Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!For this hyperbola, find the center, transverse axis, vertices, foci, and asymptotes



Ellipses And Hyperbolae




X 6 2 Y 3 2 25 The Graph In The Xy Plane Of
Textbook solution for Intermediate Algebra 10th Edition Jerome E Kaufmann Chapter Problem 35PS We have stepbystep solutions for your textbooks written by Bartleby experts!Solve the system of conic sections Involves the elimination method and a graphical understanding of the solution setOur online expert tutors can answer this problem Get stepbystep solutions from expert tutors as fast as 1530 minutes



What Is The Graph Of X 2 Y 2 Z 2 1 Quora
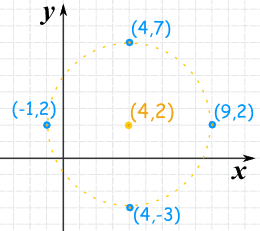



Circle Equations
Find the equation of the line tangent to the curve latexx^2y^2=25/latex at the point latex(3,4)/latex Show Solution Although we could find this equation without using implicit differentiation, using that method makes it much easierProfessionals For math, science, nutrition, historyX2 y2 = 25 x 2 y 2 = 25 This is the form of a circle Use this form to determine the center and radius of the circle (x−h)2 (y−k)2 = r2 ( x h) 2 ( y k) 2 = r 2 Match the values in this circle to those of the standard form The variable r r represents the radius of the circle, h h represents the xoffset from the origin, and k



4 2 Implicit Differentiation




Sketch The Graph Of Y X 3 2 25 Then Select The Graph That Corresponds To Your Brainly Com
Type your response in the box Imagine that this graph represents the distance Brianna travels to get to her babysitting job with respect to timeClick here👆to get an answer to your question ️ The graph of the equation x^2 y^2 = 25 includes how many points (x, y) in the coordinate plane where x and y are both integersAnswer to a Graph the equations of the system b Solve the system by using the substitution method x^2 y^2 = 25 \\x y = 1 By signing up,




Please Help Urgent Which Graph Shows The Graph Of A Circle With Equation X2 Y 5 2 25 Brainly Com




Exercises On Ellipses Centered At The Origin
Multiply x 2 y 2 y 2 − 2 x y x 2 times − x y − 2 x by multiplying numerator times numerator and denominator times denominator Cancel out x in both numerator and denominator Cancel out x in both numerator and denominator Factor the expressions that are not already factoredThe circle of x^2 y^2 = 25 has a radius of 5 units and the center of the circle is at the point (0,0) to graph the circle you solve for y equation would be y = / sqrt (25x^2) and would look like this on the graph The equation of the radius intersecting the circle atSee the answer what kind of graph is x^2y^2z^2=9 Best Answer 100% (2 ratings) Previous question Next question Get more help from Chegg Solve it with our calculus problem solver and calculator




Pin On Rayray Teaches Math
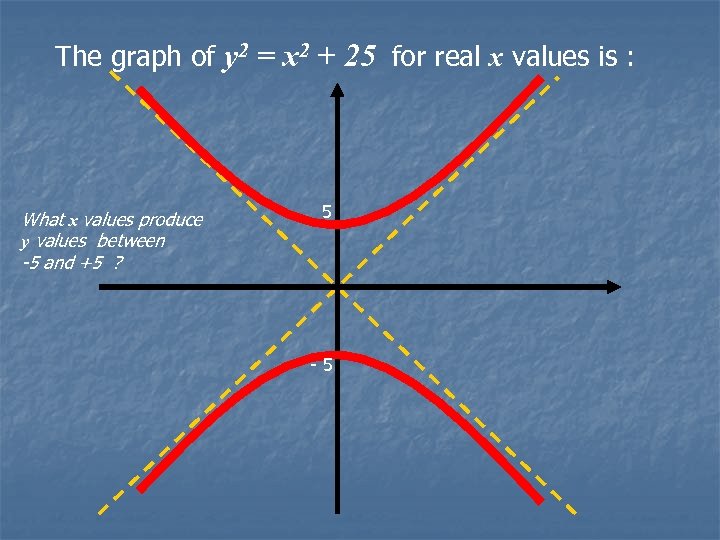



Phantom Graphs Part 2 Philip Lloyd Epsom Girls
√ 25 − (x−4)2 So when we plot these two equations we should have a circle y = 2 √ 25 − (x−4)2 y = 2 − √ 25 − (x−4)2 Try plotting those functions on the Function Grapher It is also possible to use the Equation Grapher to do it all in one goNumber of solutions tells the number of points at which line cuts the curve (here it is circle), and in case of a tangent, the solution will be just one point Here as 3x 4y −25 = 0 is equation of line, we have y = − 3 4 x 25 4 and putting this value in x2 y2 = 25, we get x2 ( − 3 4 x 25 4)2 = 25 or x2 9 16x2 − 2 ×2x2y=4 Geometric figure Straight Line Slope = 1 xintercept = 2/1 = 0000 yintercept = 2/1 = 0000 Rearrange Rearrange the equation by subtracting what is to the right of the




X 6 2 Y 3 2 25 The Graph In The Xy Plane Of The Equation Above Is A Circle If The Circle Is Translated Downward A Units Such That



Graph X 2 Ky 2 25 For Different Values Of K
Answer to Find the vertices and foci of the ellipse x^2 25y^2 = 25 Sketch its graph By signing up, you'll get thousands of stepbystepDoes the point (4, 2) lie inside or outside or on the circle x^2 y^2 = 25?Divide 0 0 by 4 4 Multiply − 1 1 by 0 0 Add − 25 25 and 0 0 Substitute the values of a a, d d, and e e into the vertex form a ( x d) 2 e a ( x d) 2 e Set y y equal to the new right side Use the vertex form, y = a ( x − h) 2 k y = a ( x h) 2 k, to determine the values of a a, h h, and k k




Finding Tangent Line To Graph Math Forums



Solution Sketch The Graph Of The Hyperbola Y 2 25 X 2 4 1 Draw The Fundamental Rectangle Find The Equations Of The Asymptotes And Label The Asymptotes On Your Graph
X2y2=25 Simple and best practice solution for X2y2=25 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve itSo we are given 2 equations mathx^2 y^2 = 25/math mathxy = 12/math And wish to find all possible solutions for this Let us start by using the second equation and solving for y mathy = \frac{12}{x}/math Which gives mathx^2 \frSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more



Solution X 2 25 Y 2 16 1 How To Graph That Ellipse
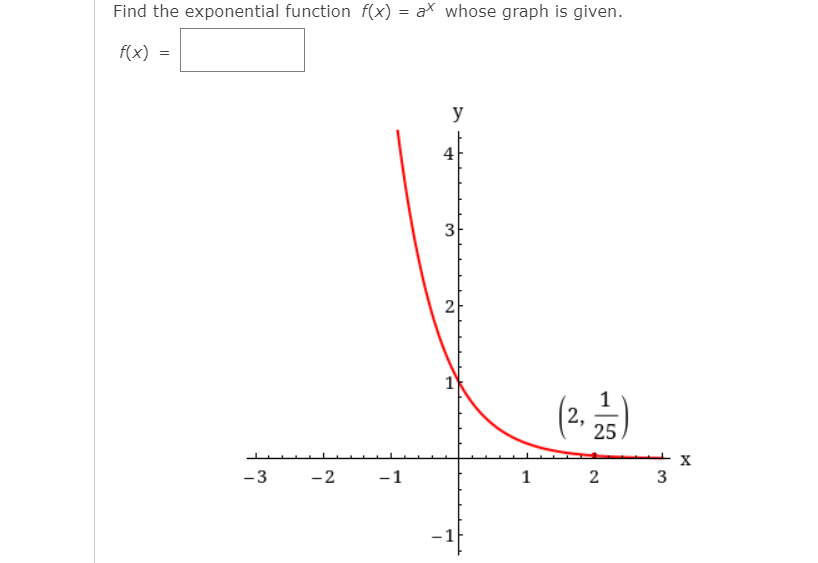



Answered Find The Exponential Function F X Ax Bartleby
Regents Exam Questions GGPEA1 Equations of Circles 4a Name _____ wwwjmaporg 3 9 Circle O is graphed on the set of axes below Which equation represents circle O?It will plot functions given in the form y = f(x), such as y = x 2 or y = 3x 1, as well as relations of the form f(x,y) = g(x,y), such as x 2 y 2 = 4 To use the plot command, simply go to the basic plot page , type in your equation (in terms of x and y), enter the set of x and y values for which the plot should be made and hit the Plot1) (x 1)2 (y −3)2 =92) (x −1)2 (y 3)2 =93) (x 1)2 (y −3)2 =64) (x −1)2 (y 3)2 =610 What is



Graphing A Circle Help Mathskey Com



Solution Graph The Solution Set X 4 2 Y 3 2 Lt 25
On the same graph paper, plot 7 graphs of x 2 k*y 2 = 25 for values of k = 4, 1, 1/4, 0, 1/4, 1, 4/chapter 6 For example, if k=4, the equation to graph is x 2 4*y 2 = 25 The graph looks like this Notice, the graph is an ellipse, the semimajor axis is 5, the semiminor axis is 5/2, and the foci are at (25*Sqrt(3),0) and (25*sqrt(3),0)Now you make the other graphs using the otherCoordinates of Center b Radius C Graph the circle Note Plot the center and then a point on the circle 7 6 5 2 7 * 1236 78 2 3 6 Clear All Draw Submit Question 8 5 6 4 2 3 U W E R Complete the information for the circle with equation (x 2)2 (y – 1)2 = 49 a Coordinates of Center b Radius c Graph the circleX^2 y^2 = 25 Choose (x,y) be a point on the graph dy/dx (x,y) can be positive, negative, 0, undefined Find formula for dy/dx using implicit differentiation Check the derivative by evaluating different points around the circle Confirm that the derivative function



2




Graph The Circle X 4 2 Y 2 2 25 Label The Center And At Least Four Points In The Circle Study Com
Get an answer for 'In how many points do the graphs of the equations x^2 y^2 = 25 and y^2 = 4x intersect?' and find homework help for other Math questions at eNotesUse the other equation x^2 y^2 = 25 Substitute 2x 5 to y then solve for x 3 Substitute the result from step 2X^ {2}y^ {2}25=0 Subtract 25 from both sides x=\frac {0±\sqrt {0^ {2}4\left (y^ {2}25\right)}} {2} This equation is in standard form ax^ {2}bxc=0 Substitute 1 for a, 0 for b, and 25y^ {2} for c in the quadratic formula, \frac {b±\sqrt {b^ {2}4ac}} {2a} x=\frac {0±\sqrt {4\left (y^ {2}



Vertices And Asymptotes To Graph Each X 2 16 Chegg Com



Geometry 10 6 Equations Of A Circle Ppt Download
Answer by Fombitz () ( Show Source ) You can put this solution on YOUR website!There can be two square roots!) Move the −2 to the right y = 2 ±Y = 3/4x25/4 We could use calculus but first as with all Mathematical problems one should step back and think about what the question is asking you, and in this case we can easily answer the question using knowledge of the equation, in this case x^2 y^2 = 25 represents a circle of centre (a,b)=(0,0) and radius r=5 First verify that (3,4) actually lies on the circle;




Which Is The Graph Of X 2 4 Y 2 25 1 Brainly Com



Y Squareroot 25 X 2 From 0 To But Since Y 2 Chegg Com
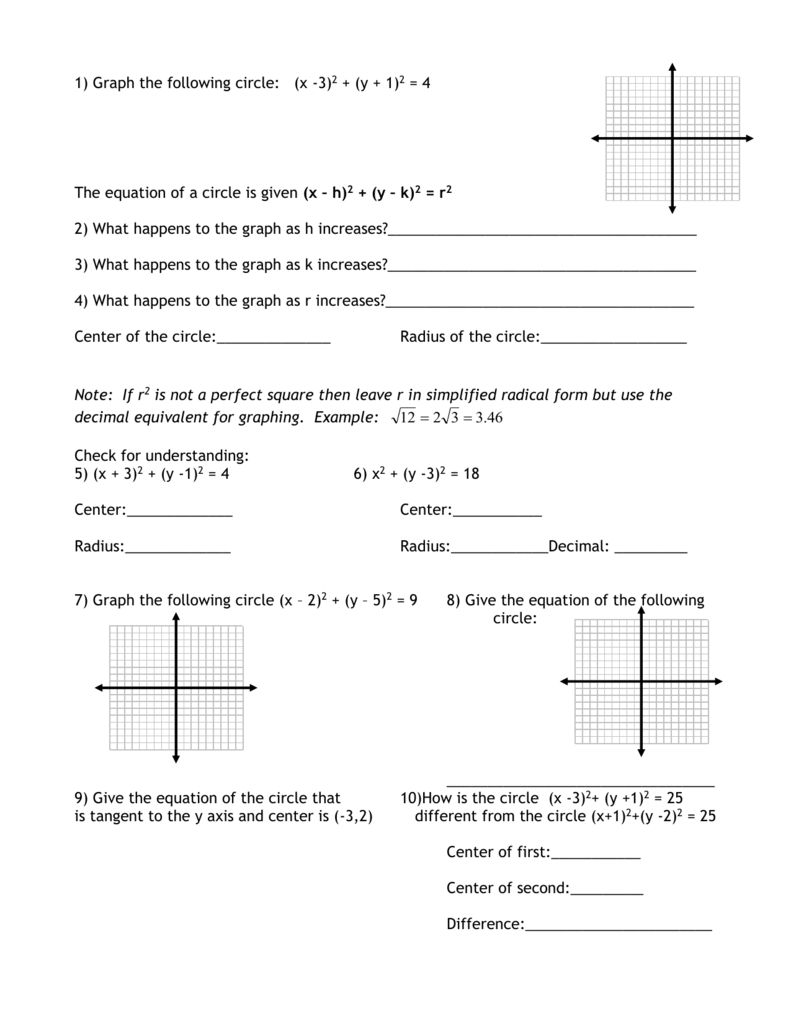
Below The general formula of a circle is given by (xh)^2(yk)^2=r^2 where (h,k) is the centre is r is the radius Therefore, x^2y^2=25 can also be written as (x0)^2(y0)^2=5^2 We can immediately see that the centre is (0,0) and the radius is 5 The graph is drawn below graph{x^2y^2=25 10, 10, 5, 5}Steps by Finding Square Root { x }^ { 2 } 2y=25 x 2 2 y = 2 5 Subtract 2y from both sides Subtract 2 y from both sides x^ {2}=252y x 2 = 2 5 − 2 y Take the square root of both sides of the equation Take the square root of both sides of the equationGraph x^2y^2=25 x2 y2 = 25 x 2 y 2 = 25 This is the form of a circle Use this form to determine the center and radius of the circle (x−h)2 (y−k)2 = r2 ( x h) 2 ( y k) 2 = r 2 Match the values in this circle to those of the standard form The variable r r represents the radius of the circle, h h represents the xoffset from the origin, and k k represents the yoffset from origin




Implicit Differentiation




If R X Y X Y In W X 2 Y 2 25 Then Find The Domain An
Find the x and y intercepts To find the xintercept, set y=0 and solve for x (5,0) and (5,0) To find the yintercept, setCompute answers using Wolfram's breakthrough technology &



Solution Stuck On How To Solve This Simultaneous Equation X 2 Y 2 25 X Y 7 Asap Please Thank You




The Ellipse X 2 169 Y 2 25 1 Has The Same Eccentricity As Th




Hyperbolas




Surfaces Part 2




2 1 R 2 16 R 0 0 R 2 25 R Special Pythagorean Triple Ppt Download
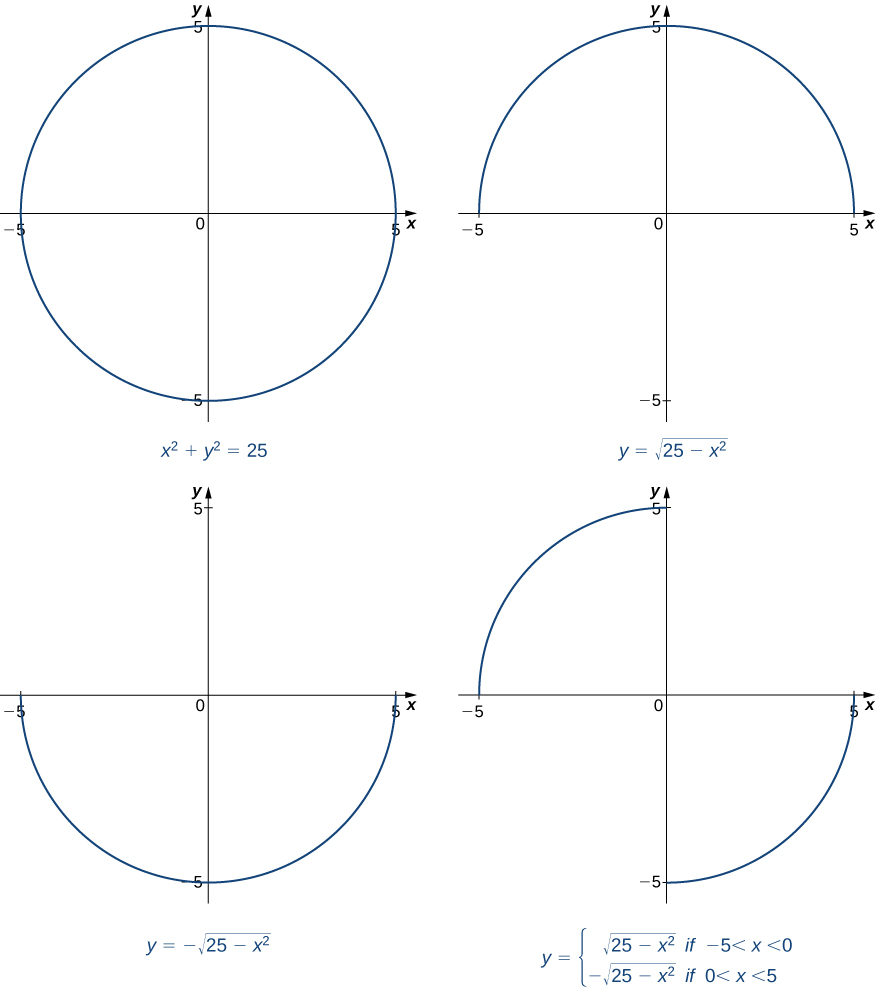



3 8 Implicit Differentiation Calculus Volume 1



Features Graph




Solve System X 2 Y 2 25 Y X 2 5 Youtube



Graph Plotting In Python Set 1 Geeksforgeeks
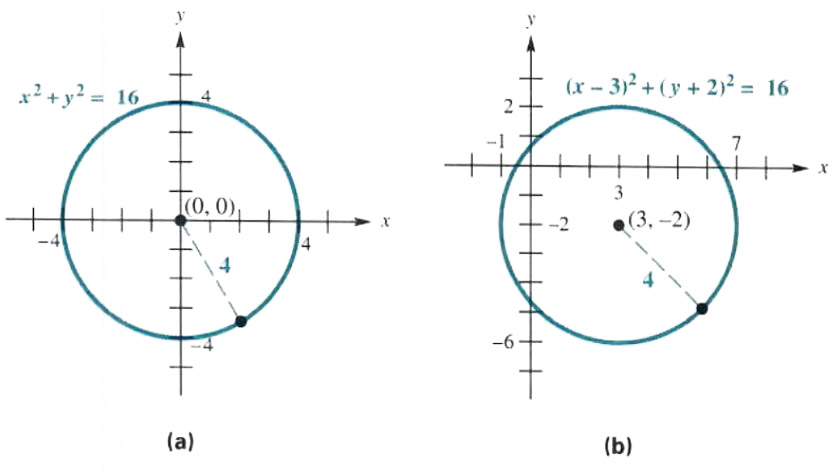



Solve The Circle And Symmetry Step By Step Math Problem Solver



10 Points To The Person Who Can Help Me With 4 Precalculus Questions Please Mathskey Com
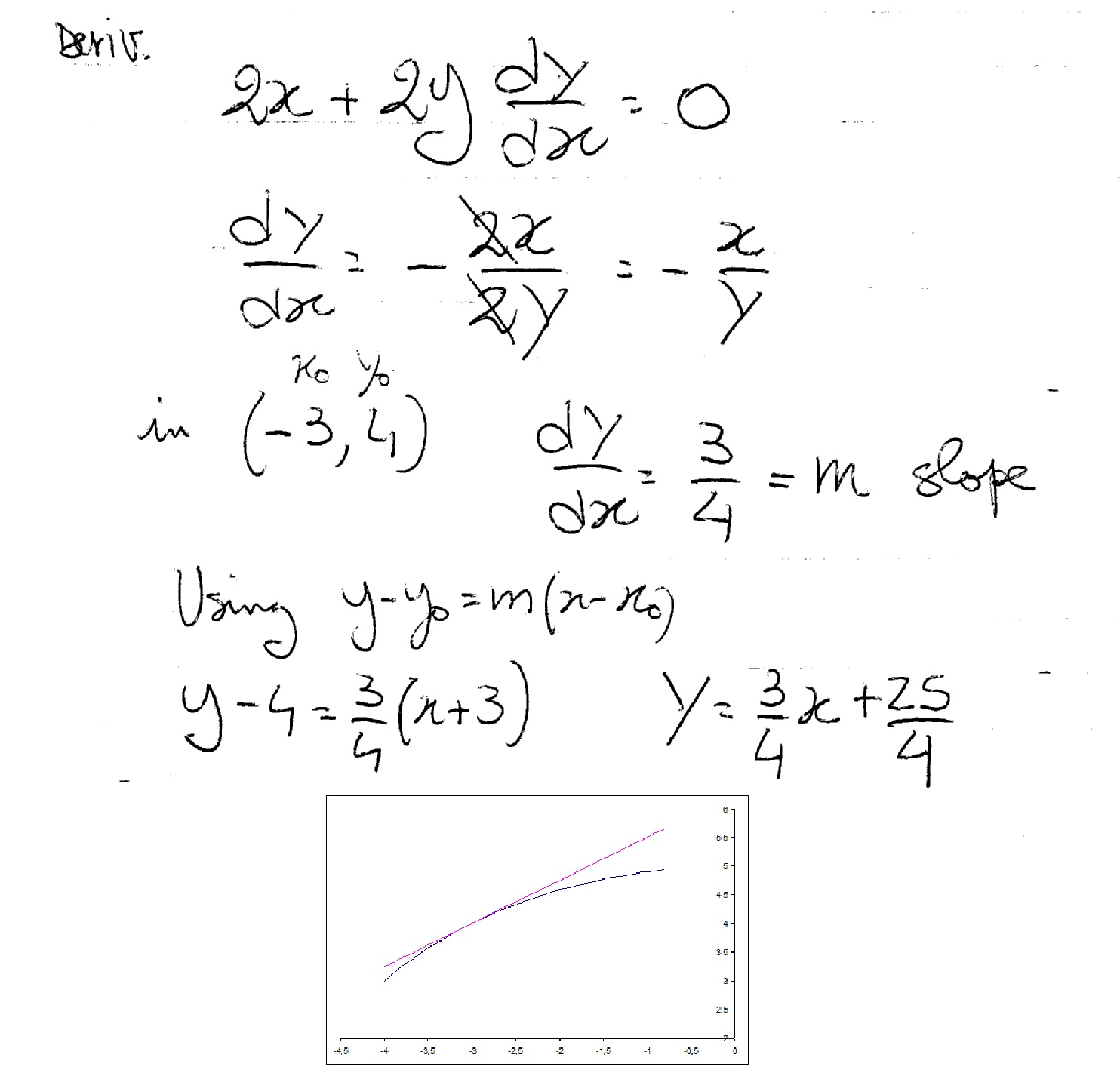



How Do You Find Equation Of Tangent To Circle X 2 Y 2 25 At The Point 3 4 Socratic



12 6 Quadric Surfaces Mathematics Libretexts



The Area Of The Region Bounded By The Ellipse X2 25 Y2 16 1 Is Studyrankersonline



Q Tbn And9gcqrtmhgysaakscrw Nolvz3a1qpo2sb Gorfekohspslxj99rif Usqp Cau




Find The Point S Where The Tangent S To The Graph Of Y X 2 25 3 Are Parallel To The X Axis Mathematics Stack Exchange



Hyperbola X 2 25 Y 2 9 1 Youtube




Which Graph Shows The Graph Of A Circle With Equation X 2 Y 4 2 16 Brainly Com



Implicit Differentiation




Graph X 2 Y 2 4 Youtube



Find The Area Bounded By The Curves X 2 Y 2 25 4y 4 X 2 And X 0 Above The X Axis Sarthaks Econnect Largest Online Education Community




Find The Area Of The Portion Of The Sphere X 2 Y 2 Z 2 25 Inside The Cylinder X 2 Y 2 9 Study Com



Graph X 2 Ky 2 25 For Different Values Of K
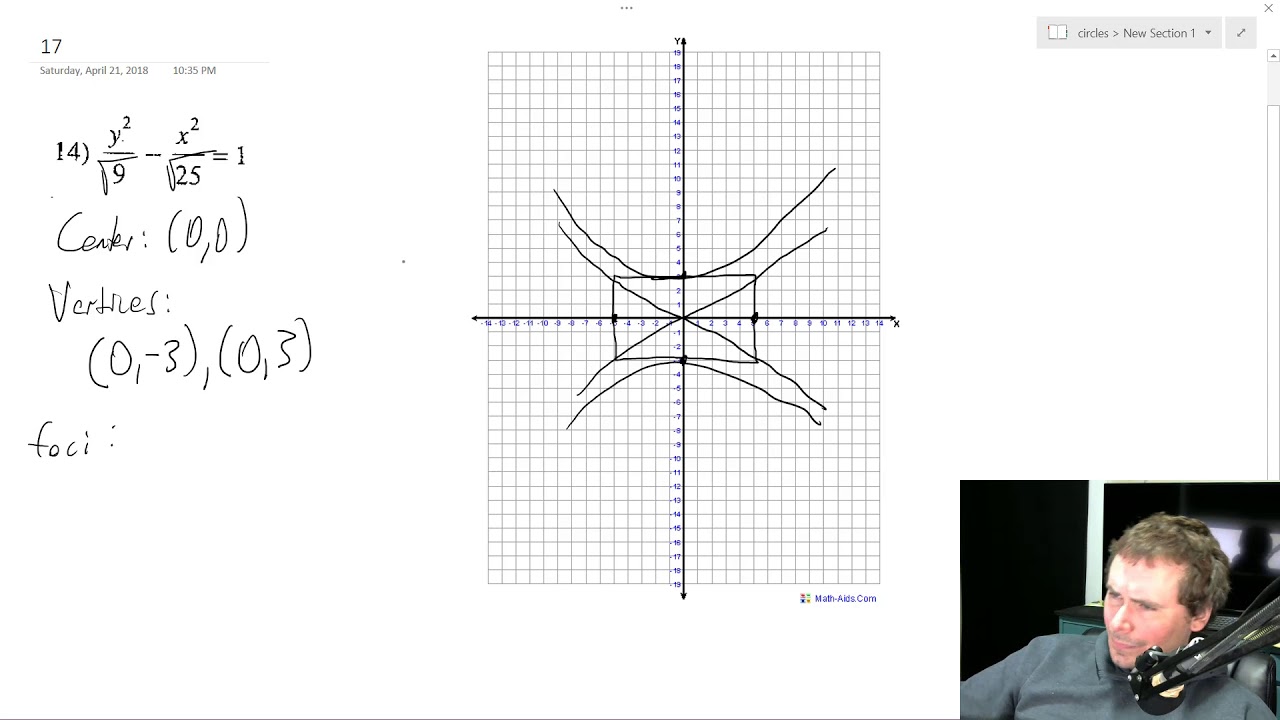



Find The Vertices Of Foci Of Y 2 9 X 2 25 1 Youtube
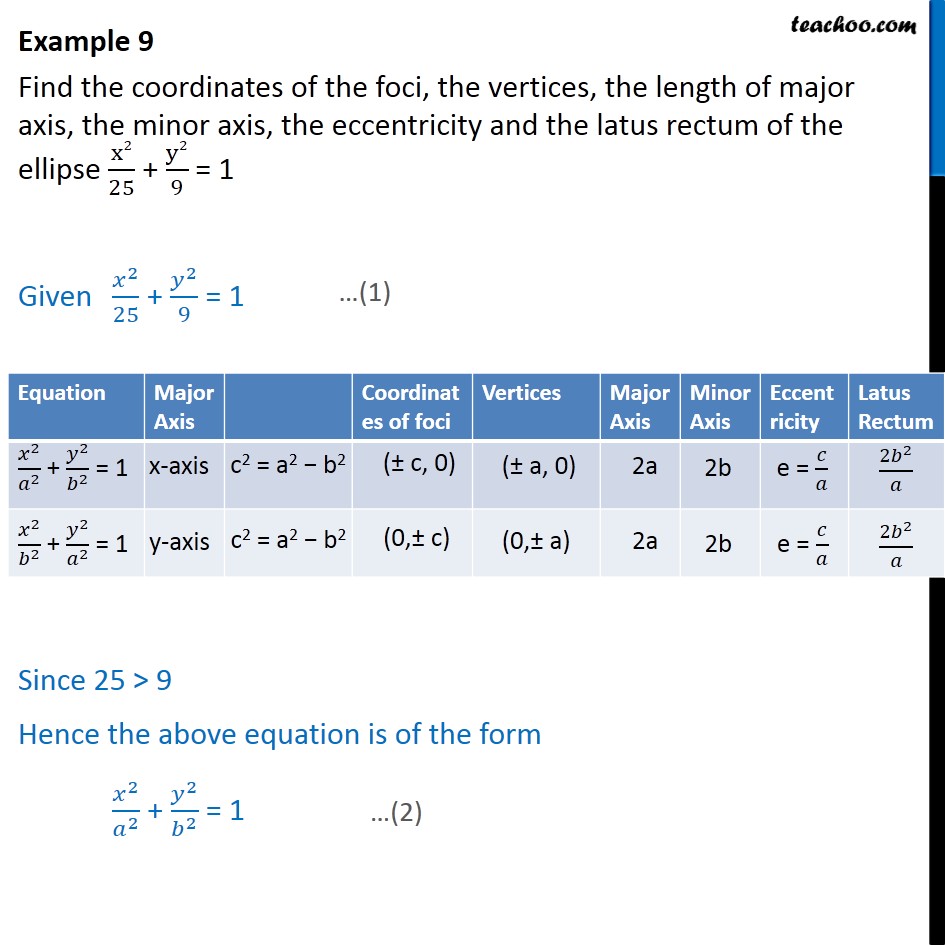



Example 9 X2 25 Y2 9 1 Find Foci Vertices Eccentricity



What Is The Solution To X 2 Y 2 25 Xy 12 Quora



Graph Y X 7 X 3 Mathskey Com




Solved Sketch The Graph Of Y X 3 2 25 Then Select The Graph That Corresponds To Your Brainly Com



Content The Concept Of A Function



Graph X 2 Ky 2 25 For Different Values Of K



Solution Graph Y 2 25 X 2 4 1
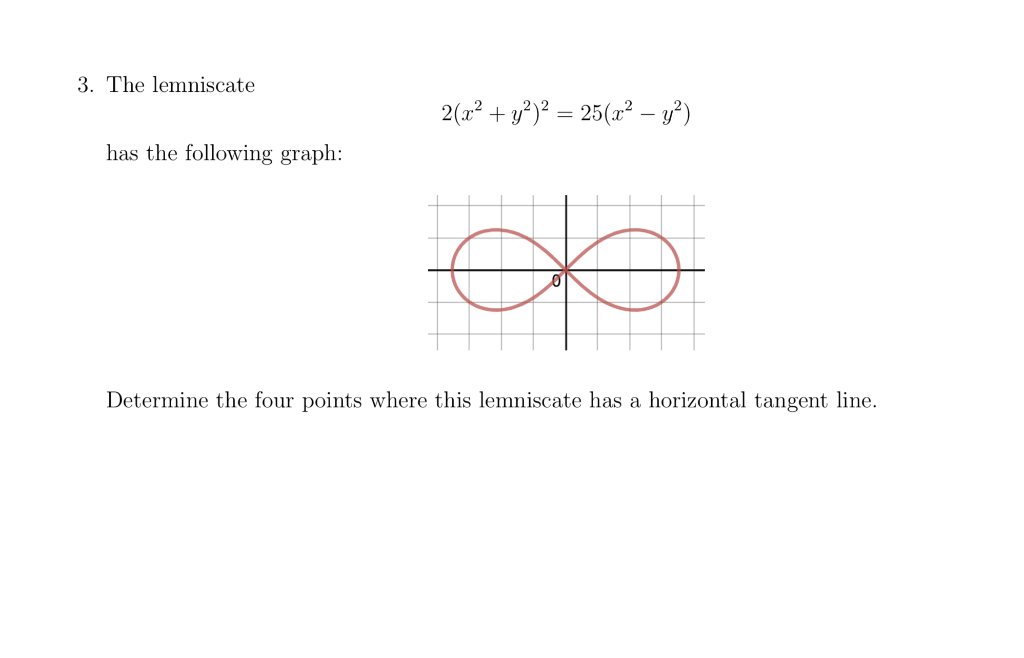



The Lemniscate 2 X 2 Y 2 2 25 X 2 Y 2 Has The Chegg Com




Warmup 1find The Values Of X For




Q16 Answers Paper 2 June 18 Edexcel Gcse Maths Higher Elevise




10 What Is The Equation Of The Circle Represented By Chegg Com




Properties Of Functions Y F X Read Y As A Function Of X X Values Independent Variables Y Valuesdependent Variables Domain Of Fall Possible Inputs X Ppt Download



How Do You Write The Definite Integral To Find The Class 12 Maths Cbse



Surfaces Part 2



2



Graph X 2 Ky 2 25 For Different Values Of K
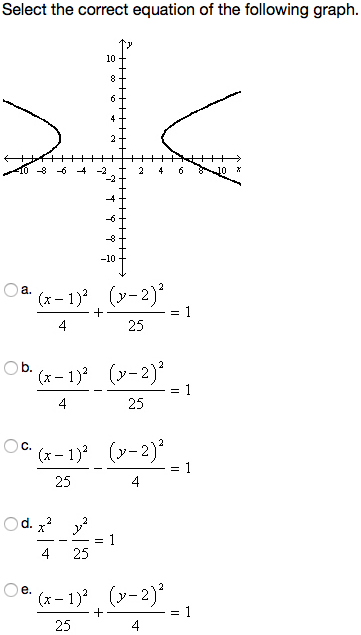



Solved Select The Correct Equation Of The Following Graph Chegg Com



1



View Question Which Graph Shows The Graph Of A Circle With Equation X2 Y 5 2 25




A Find And Identify The Traces Of The Quadric Surface X 2 Y 2 Z 2 25 Given The Plane X K Find The Trace Identify The Trace Y K



Www Npsk12 Com Cms Lib Va Centricity Domain 37 Geometry Pdf




Identify The Type Of Graph That Each Equation Has Chegg Com



Solution Sketch The Graph Of X 2 2 Y 3 2 25




View Question Which Graph Shows The Graph Of A Circle With Equation X2 Y 5 2 25



1



Content The Concept Of A Function




Geometry Mini Lesson Circle C Is Defined By The Equation X 4 2 2 Y 5 1 2 36 Which Of The Following Identifies The Center C H K And Radius Ppt Download
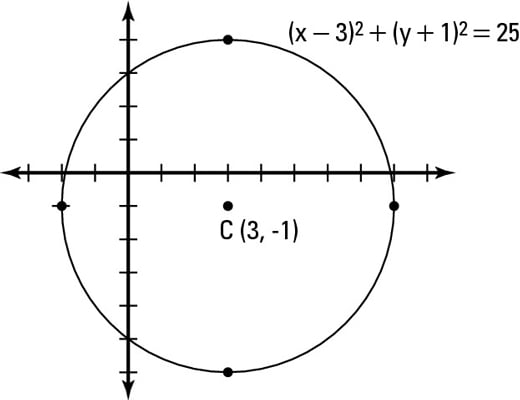



How To Graph A Circle Dummies




Graphing Parabolas




Is X 2 Y 2 25 A Function Mathematics Stack Exchange
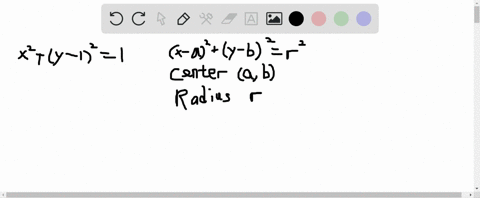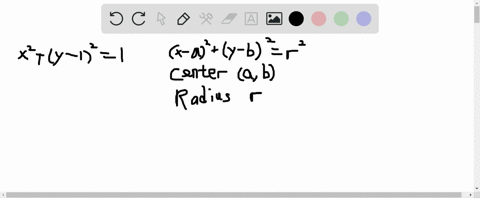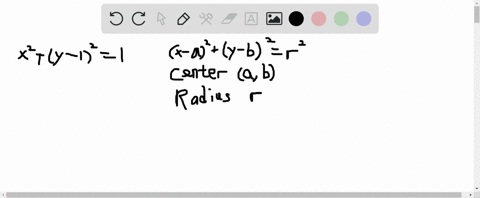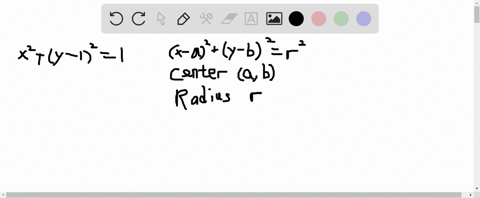



Solved 3 16 Graph The Inequality X 2 Y 2 L



How Do You Solve The System X 2y 1 And X 2 Y 2 25 By Graphing Socratic



1 Graph The Following Circle X




Equation For 3d Graphing Of Ellipsoid With That Has 2 Open Ends Opposite Each Other Stack Overflow




Equation Of Tangent Line On Circle X 1 2 Y 2 2 25 Youtube



Graphing Quadratic Functions Mathbitsnotebook Ccss Math



1




Graphing Parabolas



If A X Y X2 Y2 25 And B X Y X2 16y2 1




Inverse Of Relations Circles X 2 2 Y 2 25 And Ellipse Youtube



Solution Find The Vertices And Foci Of The Hyperbola Draw The Graph Y 2 25 X 2 21 1 X 2 9 Y 2 16 1



Solution X2 Y2 25 Is Solving This Problem Considered A Function How Do I Plot A Graph Using A Smooth Curve For This Problem Ed
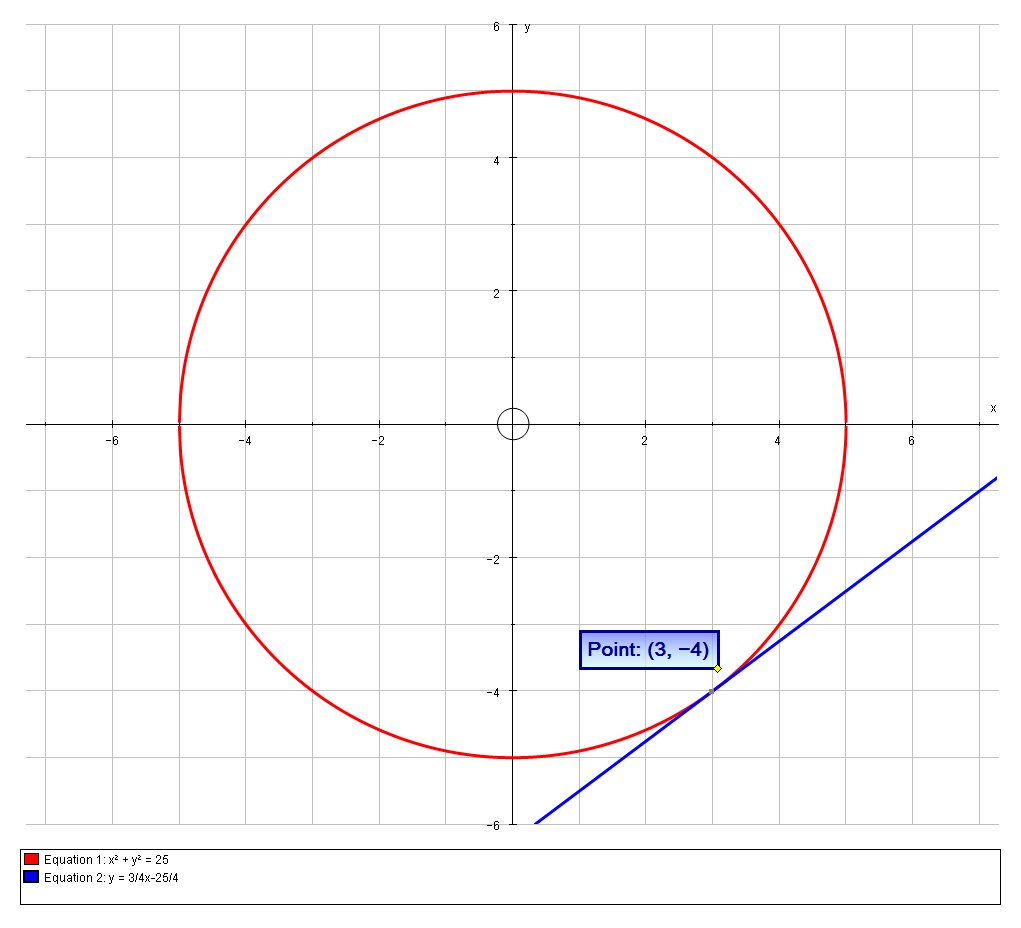



How Do You Find An Equation For The Line Tangent To The Circle X 2 Y 2 25 At The Point 3 4 Socratic
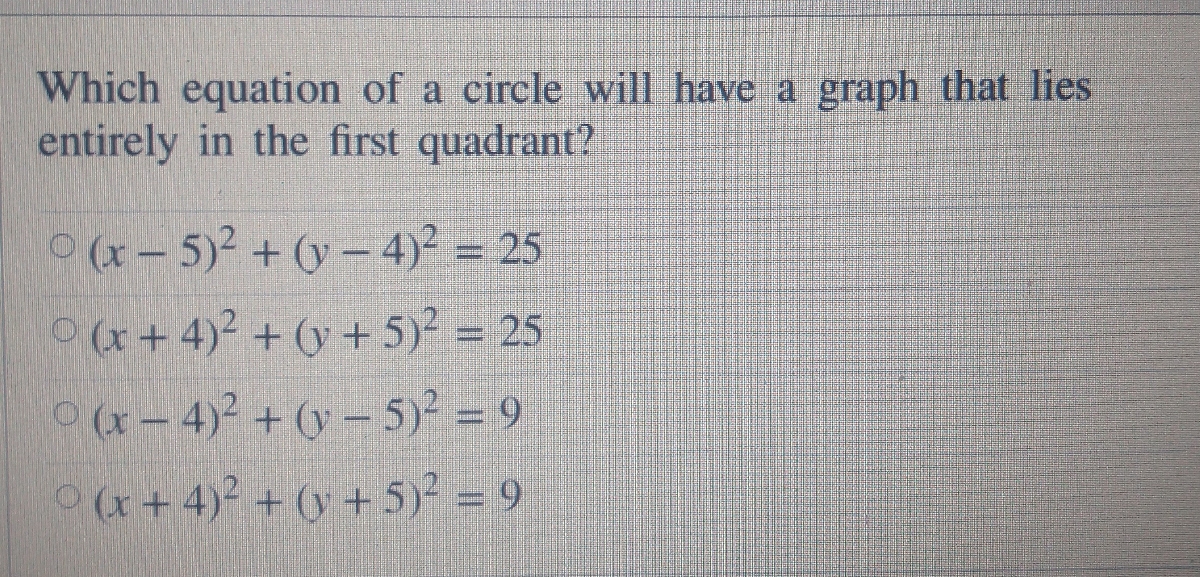



Answered Which Equation Of A Circle Will Have A Bartleby
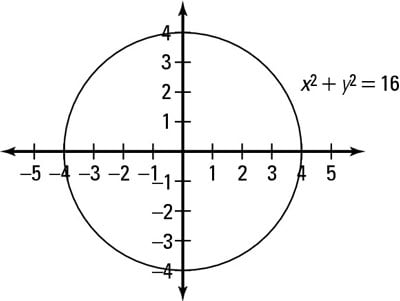



2 Ways To Graph A Circle Dummies




2 3 Equation Of A Circle How Is




Solution What Is The Equation Of The Normal To The Curve X 2 Y 2 25 At 4 3
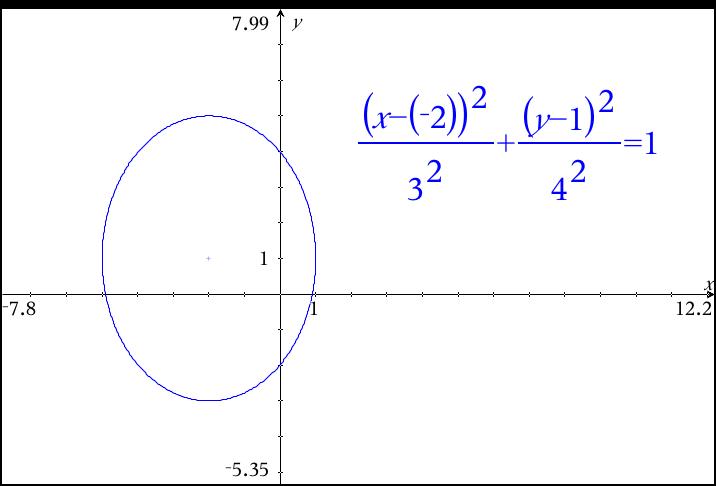



How Do I Graph X 2 2 9 Y 1 2 16 1 Algebraically Socratic
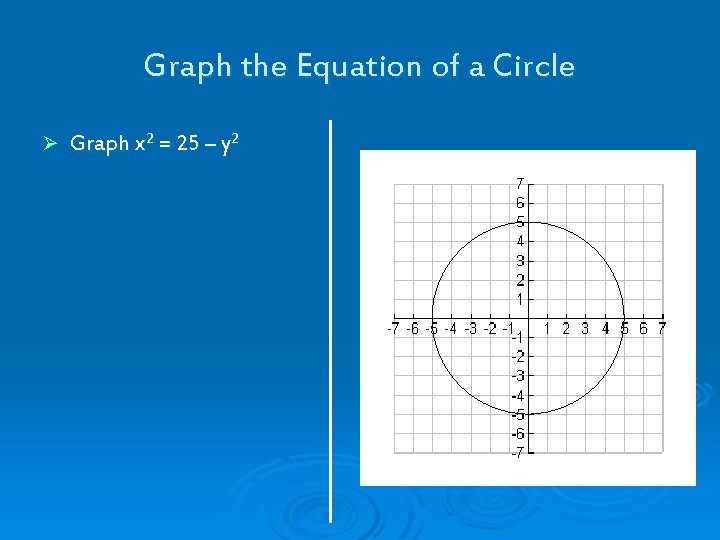



5 2 Graph And Write Equations Of Circles




Implicit Differentiation



The Hyperbola Algebra And Trigonometry



Solved Consider The Equation X2 Y 2 2 1 And The Relation X Y R 0 2 Where The R Is Read As Has Distance 1 Of Does This Equation Deter Course Hero



0 件のコメント:
コメントを投稿